题目内容
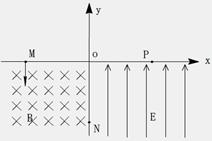
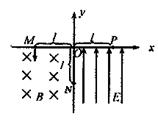
 如图所示,在x<0且y<0的区域内存在垂直纸面向里的匀强磁场,磁感应强度大小为B,在x>0且y<0的区域内存在沿y轴正方向的匀强电场.一质量为m、电荷量为q的带电粒子从x轴上的M点沿y轴负方向垂直射入磁场,结果带电粒子从y轴的N点射出磁场而进入匀强电场,经电场偏转后打到x轴上的P点,已知
如图所示,在x<0且y<0的区域内存在垂直纸面向里的匀强磁场,磁感应强度大小为B,在x>0且y<0的区域内存在沿y轴正方向的匀强电场.一质量为m、电荷量为q的带电粒子从x轴上的M点沿y轴负方向垂直射入磁场,结果带电粒子从y轴的N点射出磁场而进入匀强电场,经电场偏转后打到x轴上的P点,已知| OM |
| ON |
| OP |
(1)带电粒子进入匀强磁场时初速度的大小;
(2)带电粒子从射入匀强磁场到射出匀强电场所用的时间;
(3)匀强电场的场强大小.
分析:(1)根据粒子在磁场中匀速圆周运动,洛伦兹力提供向心力,结合牛顿第二定律,即可求解;
(2)根据粒子在磁场中做匀速圆周运动,在电场中做类平抛运动,结合前者由周期与圆心角求解,后者由运动学公式求出,从而可求出总时间;
(3)根据粒子在电场中作类平抛运动,由牛顿第二定律与运动学公式相结合,即可求解.
(2)根据粒子在磁场中做匀速圆周运动,在电场中做类平抛运动,结合前者由周期与圆心角求解,后者由运动学公式求出,从而可求出总时间;
(3)根据粒子在电场中作类平抛运动,由牛顿第二定律与运动学公式相结合,即可求解.
解答:解:(1)设带电粒子射入磁场时的速度大小为v,
由带电粒子射入匀强磁场的方向和几何关系可知,
带电粒子在磁场中做圆周运动,圆心位于坐标原点,半径为l,
则有:Bqv=m
,
解得:v=
(2)设带电粒子在磁场中运动时间为t1,在电场中运动的时间为t2,总时间为t,
则有t1=
=
;
而t2=
=
所以t=
;
(3)带电粒子在电场中做类平抛运动,
位移关系式,l=
at2
时间t2=
加速度为a=
联立可解得:E=
答:(1)带电粒子进入匀强磁场时初速度的大小v=
;
(2)带电粒子从射入匀强磁场到射出匀强电场所用的时间
;
(3)匀强电场的场强大小
.
由带电粒子射入匀强磁场的方向和几何关系可知,
带电粒子在磁场中做圆周运动,圆心位于坐标原点,半径为l,
则有:Bqv=m
| v2 |
| l |
解得:v=
| Bql |
| m |
(2)设带电粒子在磁场中运动时间为t1,在电场中运动的时间为t2,总时间为t,
则有t1=
| T |
| 4 |
| πm |
| 2Bq |
而t2=
| l |
| v |
| m |
| Bq |
所以t=
| (π+2)m |
| 2Bq |
(3)带电粒子在电场中做类平抛运动,
位移关系式,l=
| 1 |
| 2 |
时间t2=
| l |
| v |
加速度为a=
| qE |
| m |
联立可解得:E=
| 2B2lq |
| m |
答:(1)带电粒子进入匀强磁场时初速度的大小v=
| Bql |
| m |
(2)带电粒子从射入匀强磁场到射出匀强电场所用的时间
| (π+2)m |
| 2Bq |
(3)匀强电场的场强大小
| 2B2lq |
| m |
点评:考查带电粒子在电场中做类平抛运动,在磁场中做匀速圆周运动,掌握圆周运动与类平抛运动的处理规律,注意几何关系的正确运用,最后理解牛顿第二定律在题中的应用.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目

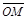 =
=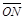 =
=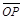 =l。
=l。