题目内容
 如图所示,用长为L=0.8m的轻质细绳将一质量为1kg的小球悬挂在距离水平面高为H=2.05m的O点,将细绳拉直至水平状态无初速度释放小球,小球摆动至细绳处于竖直位置时细绳恰好断裂,小球落在距离O点水平距离为2m的水平面上的B点,不计空气阻力,取g=10m/s2.求:
如图所示,用长为L=0.8m的轻质细绳将一质量为1kg的小球悬挂在距离水平面高为H=2.05m的O点,将细绳拉直至水平状态无初速度释放小球,小球摆动至细绳处于竖直位置时细绳恰好断裂,小球落在距离O点水平距离为2m的水平面上的B点,不计空气阻力,取g=10m/s2.求:(1)绳子断裂后小球落到地面所用的时间;
(2)小球落地的速度的大小;
(3)绳子能承受的最大拉力.
分析:(1)细绳断裂后,小球做平抛运动,根据平抛运动的规律即可求解;
(2)求出小球落地时的水平速度和竖直速度,即可求解;
(3)小球运动到A点时,绳子刚好断了,此时绳子的拉力即为最大拉力,根据向心力公式即可求解.
(2)求出小球落地时的水平速度和竖直速度,即可求解;
(3)小球运动到A点时,绳子刚好断了,此时绳子的拉力即为最大拉力,根据向心力公式即可求解.
解答:解:(1)细绳断裂后,小球做平抛运动,竖直方向自由落体运动,则:
竖直方向:hAB=
gt2
解得:t=
s=0.5s
(2)水平方向匀速运动,
v0=
=
m/s=4m/s
vy=gt=5m/s
所以v=
=
m/s≈6.4m/s
(3)在A点根据向心力公式得:
T-mg=m
T=mg+m
=10+20N=30N
答:(1)绳子断裂后小球落到地面所用的时间为0.5s;(2)小球落地的速度的大小为6.4m/s;(3)绳子能承受的最大拉力为30N.
竖直方向:hAB=
| 1 |
| 2 |
解得:t=
|
(2)水平方向匀速运动,
v0=
| x |
| t |
| 2 |
| 0.5 |
vy=gt=5m/s
所以v=
| v02+vy2 |
| 41 |
(3)在A点根据向心力公式得:
T-mg=m
| v02 |
| L |
T=mg+m
| v02 |
| L |
答:(1)绳子断裂后小球落到地面所用的时间为0.5s;(2)小球落地的速度的大小为6.4m/s;(3)绳子能承受的最大拉力为30N.
点评:该题主要考查了平抛运动的基本规律及向心力公式,难度不大,属于基础题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
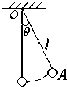 如图所示,用长为l的绳子一端系着一个质量为m的小球,另一端固定在O点,拉小球至A点,此时绳偏离竖直方向θ,松手后小球经过最低点时的速率为( )(空气阻力不计)
如图所示,用长为l的绳子一端系着一个质量为m的小球,另一端固定在O点,拉小球至A点,此时绳偏离竖直方向θ,松手后小球经过最低点时的速率为( )(空气阻力不计)A、
| ||
B、
| ||
C、
| ||
D、
|
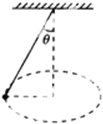 如图所示,用长为L的细线拴一个质量为M的小球,使小球在水平面内做匀速圆周运动,细线与竖直方向间的夹角为θ,关于小球的受力情况,下列说法正确的是( )
如图所示,用长为L的细线拴一个质量为M的小球,使小球在水平面内做匀速圆周运动,细线与竖直方向间的夹角为θ,关于小球的受力情况,下列说法正确的是( )| A、小球受到重力、线的拉力和向心力三个力 | B、向心力的大小等于细线对小球拉力的大小 | C、向心力的大小等于重力的大小 | D、向心力是细线的拉力和小球所受重力的合力 |
 如图所示,用长为L的细线栓着一质量为m的小球,使小球在水平面内做匀速圆周运动,细线与竖直方向间的夹角为θ.下列说法中正确的( )
如图所示,用长为L的细线栓着一质量为m的小球,使小球在水平面内做匀速圆周运动,细线与竖直方向间的夹角为θ.下列说法中正确的( ) 如图所示,用长为L的细绳拴着质量为m的小球在竖直平面内做圆周运动,则( )
如图所示,用长为L的细绳拴着质量为m的小球在竖直平面内做圆周运动,则( ) 如图所示,用长为L的细线拴一个质量为M的小球,使小球在水平面内做匀速圆周运动,细线与竖直方向间的夹角为0,关于小球的受力情况,下列说法正确的是( )
如图所示,用长为L的细线拴一个质量为M的小球,使小球在水平面内做匀速圆周运动,细线与竖直方向间的夹角为0,关于小球的受力情况,下列说法正确的是( )