题目内容
(12分)如图11所示,光滑的水平地面上有一木板,其左端放有一重物,右方有一竖直的墙。重物质量为木板质量的2倍,重物与木板间的动摩擦因数为![]() 。使木板与重物以共同的速度v0向右运动,某时刻木板与墙发生弹性碰撞,碰撞时间极短。设木板足够长,重物始终在木板上。重力加速度为g。求
。使木板与重物以共同的速度v0向右运动,某时刻木板与墙发生弹性碰撞,碰撞时间极短。设木板足够长,重物始终在木板上。重力加速度为g。求
(1)木板第一次与墙碰撞后,重物与木板的共同速度;
(2)木板从第一次与墙碰撞到第二次碰撞所经历的时间;
(3)木板从第一次与墙碰撞开始,整个运动过程所经历的时间。
(1)![]()
(2)![]()
(3)![]()
解析:木板第一次与墙碰撞后,向左匀减速直线运动,直到静止,再反向向右匀加速直线运动直到与重物有共同速度,再往后是匀速直线运动,直到第二次撞墙。
(1) 木板第一次与墙碰撞后,重物与木板相互作用直到有共同速度,动量守恒,有:
![]() ,解得:
,解得:![]()
(2) 木板在第一个过程中,用动量定理,有:![]()
用动能定理,有:![]()
木板在第二个过程中,匀速直线运动,有:![]()
木板从第一次与墙碰撞到第二次碰撞所经历的时间t=t1+t2=![]() +
+![]() =
=![]()
(3)木板从第二次与墙碰撞到第三次碰撞所经历的时间t’=t3+t4=![]()
木板从第三次与墙碰撞到第四次碰撞所经历的时间t”=t4+t5=![]()
总时间t总 =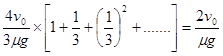

练习册系列答案
相关题目
 如图11所示,光滑弧形轨道下端与水平传送带上表面等高,轨道上的A点到传送带的竖直距离和传送带上的表面到地面的距离为均为h=5m,把一物体放在A点由静止释放,当传送带不动,物体从右端B点水平飞记,落在水平地面上的P点,B、P的水平距离OP为x=2m.g取10m/s2,求:
如图11所示,光滑弧形轨道下端与水平传送带上表面等高,轨道上的A点到传送带的竖直距离和传送带上的表面到地面的距离为均为h=5m,把一物体放在A点由静止释放,当传送带不动,物体从右端B点水平飞记,落在水平地面上的P点,B、P的水平距离OP为x=2m.g取10m/s2,求: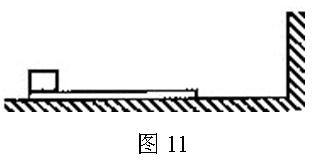
 倍,重物与木板间的动摩擦因数为
倍,重物与木板间的动摩擦因数为 。使木板与重物以共同的速度v0向右运动,某时刻木板与墙发生弹性碰撞,碰撞时间极短。设木板足够长,重物始终在木板上。重力加速度为g。求
。使木板与重物以共同的速度v0向右运动,某时刻木板与墙发生弹性碰撞,碰撞时间极短。设木板足够长,重物始终在木板上。重力加速度为g。求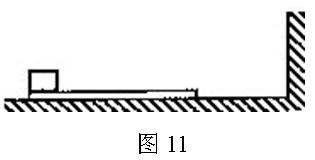
 。使木板与重物以共同的速度v0向右运动,某时刻木板与墙发生弹性碰撞,碰撞时间极短。设木板足够长,重物始终在木板上。重力加速度为g。求
。使木板与重物以共同的速度v0向右运动,某时刻木板与墙发生弹性碰撞,碰撞时间极短。设木板足够长,重物始终在木板上。重力加速度为g。求