Question

【题目】如图所示，一个小球用长为L的细线悬于O点，将小球向左拉到某一高度，此时细线与竖直方向的夹角为θ =53°，由静止释放小球，若小球向右摆动到最低点时细线断开，小球落在水平地面的A点（未画出）；若小球向右摆动到最高点时细线断开，小球的落地点也在A点，不计空气阻力，sin 530 = 0.8，则细线的悬点O离水平地面的高度为 ( )

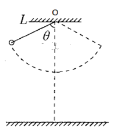
A. 1.2 L B. 1.4 L C. 1.6 L D. 1.8 L

Answer 1

【答案】B

【解析】

若小球向右摆动到最低点时细线断开，先根据机械能守恒得到小球通过最低点时的速度，结合平抛运动的规律得到平抛运动的水平距离；

若小球向右摆动到最高点时细线断开，根据机械能守恒得到小球向右摆动的最大偏角，结合几何关系求解。

设细线的悬点O离水平地面的高度为h。

若小球向右摆动到最低点时细线断开，断开前的过程，根据机械能守恒得

绳断开后小球做平抛运动，则有：

x=vt

若小球向右摆动到最高点时细线断开，根据机械能守恒得到小球向右摆动的最大偏角为53°，则有：x=Lsin53°

联立得：h=1.4L。

故应选：B。