题目内容
 两个质量相同的小球A、B,中间用轻弹簧相连,放在光滑的水平面上,A球挨着左墙壁,如图所示.若用水平向左的短时冲量I作用于B球,B球将弹簧压缩,弹簧的最大弹性势能是4J,当A球离开墙壁瞬间,B球的动量大小是2kg?m/s.则B球的质量是
两个质量相同的小球A、B,中间用轻弹簧相连,放在光滑的水平面上,A球挨着左墙壁,如图所示.若用水平向左的短时冲量I作用于B球,B球将弹簧压缩,弹簧的最大弹性势能是4J,当A球离开墙壁瞬间,B球的动量大小是2kg?m/s.则B球的质量是0.5kg
0.5kg
;水平冲量I的大小是2 N?s
2 N?s
.?分析:给B球施加冲量,弹簧压缩,当B球速度为零,弹簧压缩到最短,弹性势能最大,当弹簧恢复原长时,A离开墙壁,弹簧的弹性势能全部转化为B的动能,结合动量和动能的表达式求出B球的质量,通过B的动量大小求出水平冲量的大小.
解答:解:用水平向左的短时冲量I作用于B球后,B球获得一定的动量,向左压缩弹簧,压缩过程中,B球的动能转化为弹簧的弹性势能,机械能守恒.B球速度为零时,弹簧弹性势能最大为4 J,当A球离开墙壁瞬间,弹簧刚好恢复原长,B球动能为4 J,而B球的动量大小是2 kg?m/s,由动量公式p=mv和动能公式Ek=
mv2,可求出B球的质量?0.5 kg,同时可知B球压缩弹簧前的动量大小也是2 kg?m/s,据动量定理,水平冲量I的大小是2 N?s.?
故答案为:0.5 kg;2 N?s.
| 1 |
| 2 |
故答案为:0.5 kg;2 N?s.
点评:解决本题的关键理清小球的运动过程,知道能量的转化,以及掌握动量定理和动量与动能的关系.

练习册系列答案
相关题目
 如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则( )
如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则( )| A、球A的线速度必定大于球 B的线速度 | B、球A的角速度必定大于球B的角速度 | C、球A的运动周期必定小于球B的运动周期 | D、球A对筒壁的压力必定大于球B对筒壁的压力 |
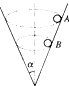 如图所示,在光滑的圆锥漏斗的内壁,两个质量相同的小球A和B,分别紧贴着漏斗在各自的水平面内做匀速圆周运动,其中小球A的位置在小球B的上方.下列判断正确的是( )
如图所示,在光滑的圆锥漏斗的内壁,两个质量相同的小球A和B,分别紧贴着漏斗在各自的水平面内做匀速圆周运动,其中小球A的位置在小球B的上方.下列判断正确的是( )| A、A球的速率等于B球的速率 | B、A球的角速度大于B球的角速度 | C、A球对漏斗壁的压力等于B球对漏斗壁的压力 | D、A球的转动周期等于B球的转动周期 |
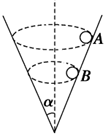 在光滑的圆锥漏斗的内壁,两个质量相同的小球A和B,分别紧贴着漏斗在水平面内做匀速圆周运动,其中小球A的位置在小球B的上方,如图所示.下列判断正确的是( )
在光滑的圆锥漏斗的内壁,两个质量相同的小球A和B,分别紧贴着漏斗在水平面内做匀速圆周运动,其中小球A的位置在小球B的上方,如图所示.下列判断正确的是( ) 如图所示,两个质量相同的小球A和B,分别用线悬在等高的O1、O2两点,A球的悬线比B球的悬线长,把两球的悬线拉到水平后将小球无初速度释放,则两球经过最低点时( )
如图所示,两个质量相同的小球A和B,分别用线悬在等高的O1、O2两点,A球的悬线比B球的悬线长,把两球的悬线拉到水平后将小球无初速度释放,则两球经过最低点时( )