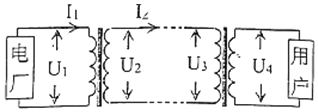
��Ŀ����
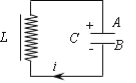
����Ŀ����ͼ��ʾ����ֱ�ᵯ��B���¶˹̶���ˮƽ���ϣ��϶���A���ӣ���ʼʱA��ֹ��A������Ϊm��2kg������B�ľ���ϵ��Ϊk1��200N/m����ϸ����������ֽ�����A����һ������ϵ��Ϊk2���ᵯ��C���ӣ�������C����ˮƽλ����δ�����α�ʱ�����Ҷ˵�λ��aλ�ã���ʱA�϶�����ǡ����ֱ��ֱ��������C���Ҷ˵���ˮƽ����������bλ��ʱ������B������A��������Сǡ�õ���A����������֪ab��60cm����
��1��������C����ˮƽλ����δ�����α�ʱ������B���α����Ĵ�С��
��2���ù���������A�����ĸ߶ȼ��ᵯ��C�ľ���ϵ��k2��
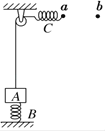
���𰸡���1��10cm����2��100N/m��
��������
��1������C����ˮƽλ����û�з����α�ʱ��A���ھ�ֹ������B����ѹ��״̬��
���ݺ��˶����У�k1x1��mg
�������ݽ�ã�x1��10cm
��2����ab��60cmʱ������B�����쳤״̬�����ݺ��˶����У�
k1x2��mg
����������ã�x2��10cm
��A�����߶�Ϊ��h��x1+x2��20cm
�ɼ��ι�ϵ�ɵõ���C���쳤��Ϊ��x3��ab��x1��x2��40cm
����ƽ����������˶����У�
mg+k1x2��k2x3
���k2��100N/m

��ϰ��ϵ�д�
 ���źþ���Ԫ����ĩ��ϵ�д�
���źþ���Ԫ����ĩ��ϵ�д�
�����Ŀ