题目内容
 一个滑板运动员,滑板和人总质量为50kg,以12m/s的速度从一斜坡底端滑上斜坡,当速度减为零时,又从斜坡上下滑至底端,已知斜坡的倾角为300,运动员上滑时用时为2s,设滑板受的阻力大小恒定不变,(g=10m/s2)求:
一个滑板运动员,滑板和人总质量为50kg,以12m/s的速度从一斜坡底端滑上斜坡,当速度减为零时,又从斜坡上下滑至底端,已知斜坡的倾角为300,运动员上滑时用时为2s,设滑板受的阻力大小恒定不变,(g=10m/s2)求:(1)滑板受到的阻力大小;
(2)运动员匀加速下滑至底端时所需的时间.
分析:(1)根据匀变速直线运动的速度时间公式求出滑板上滑的加速度,再根据牛顿第二定律求出滑板受到的阻力的大小.
(2)根据牛顿第二定律求出滑板下滑的加速度,求出上滑的位移,根据匀变速直线运动的位移时间公式求出运动员下滑的时间.
(2)根据牛顿第二定律求出滑板下滑的加速度,求出上滑的位移,根据匀变速直线运动的位移时间公式求出运动员下滑的时间.
解答:解:(1)匀减速上滑,受力分析如图,选取沿斜面向上为正方向
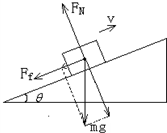
由v=v0+a1t1
得a1=
=
=-6m/s2
由牛顿第二定律可得:-(mgsinθ+Ff)=ma1
解得:Ff=50N
答:滑板受到的阻力大小为50N.
(2)匀加速下滑,受力分析如图,选取沿斜面向下为正方向
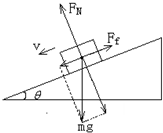
由牛顿第二定律可得:mgsinθ-Ff=ma2
代入数据可得:a2=4m/s2
运动员上滑的位移为:x=
t1 可得:x=12m
下滑的位移与上滑时的位移相同,设下滑的时间为t2
由x=
a2t22
可得 t2=
=
s
答:运动员匀加速下滑至底端时所需的时间为
s.

由v=v0+a1t1
得a1=
| v-v0 |
| t1 |
| 0-v0 |
| t1 |
由牛顿第二定律可得:-(mgsinθ+Ff)=ma1
解得:Ff=50N
答:滑板受到的阻力大小为50N.
(2)匀加速下滑,受力分析如图,选取沿斜面向下为正方向

由牛顿第二定律可得:mgsinθ-Ff=ma2
代入数据可得:a2=4m/s2
运动员上滑的位移为:x=
| v0+0 |
| 2 |
下滑的位移与上滑时的位移相同,设下滑的时间为t2
由x=
| 1 |
| 2 |
可得 t2=
|
| 6 |
答:运动员匀加速下滑至底端时所需的时间为
| 6 |
点评:加速度是联系力学和运动学的桥梁,通过加速度,可以根据力求运动,也可以根据运动求力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,一个滑板运动员,滑板和人的总质量为50kg,以某一初速度从一个斜坡底端滑上斜坡,当速度减小为零时,又从斜坡上下滑至底端,已知斜坡的倾角为30°,运动员上滑的时间是2s,设人及滑板受到的阻力(包括摩擦力和空气阻力)的大小恒为50N,g取10m/s2.求:
如图,一个滑板运动员,滑板和人的总质量为50kg,以某一初速度从一个斜坡底端滑上斜坡,当速度减小为零时,又从斜坡上下滑至底端,已知斜坡的倾角为30°,运动员上滑的时间是2s,设人及滑板受到的阻力(包括摩擦力和空气阻力)的大小恒为50N,g取10m/s2.求:
