题目内容
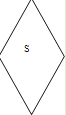
【题目】如图所示,在一个边长为l的菱形区域内,有垂直于纸面的匀强磁场,磁感应强度大小为B,菱形的一个锐角为60°.在菱形中心有一粒子源S,向纸面内各个方向发射速度大小相同的同种带电粒子,这些粒子电量为q、质量为m.如果要求菱形内的所有区域都能够有粒子到达,则下列粒子速度能够满足要求的有( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】AD
【解析】
要使粒子能够到达菱形内的所有区域,最远的是到达菱形的最上面的点和最下面的点,临界轨迹是轨迹经过菱形的顶点且与边相切,结合几何关系求解轨道半径,运用洛伦兹力等于向心力列式求解最大磁感应强度。
粒子在磁场中做匀速圆周运动,根据牛顿第二定律,有:
![]()
解得:![]()
速度越大,轨道半径越大;
临界轨迹是轨迹经过菱形的上顶点(或下顶点)且与边相切,如图所示:
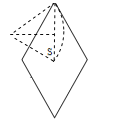
临界轨迹对应的圆心角为60°,故轨道半径为:
![]()
由于是临界轨迹,故:r≥R
联立解得:![]()
故AD正确,BC错误;
故选:AD。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目