Question

【题目】土星周围有许多大小不等的岩石颗粒,其绕土星的运动可视为圆周运动。其中有两个岩石颗粒A和B与土星中心距离分别为rA=8.0×104km和rB=1.2×105km.忽略所有岩石颗粒间的相互作用,求：(结果可用根式表示)

（1）求岩石颗粒A和B的线速度之比；

（2）求岩石颗粒A和B的周期之比；

（3）土星探测器上有一物体,在地球上重为10N,推算出他在距土星中心3.2×105km处受到土星的引力为0.38N.已知地球半径为6.4×103km，请估算土星质量是地球质量的多少倍?

Answer 1

【答案】（1）（2）（3） 95(倍)

【解析】试题分析：（1）由万有引力提供向心力即可列式求解；

（2）同样根据万有引力提供向心力列式求解；

（3）根据万有引力公式直接列式比较即可求解．

解：（1）设土星质量为M0，颗粒质量为m，颗粒距土星中心距离为r，线速度为v，据牛顿第二定律和万有引力定律有

解得

对于A、B两颗粒分别有

解得

故岩石颗粒A和B的线速度之比为：2．

（2）设颗粒绕土星作圆周运动的周期为T，则有

对于A、B两颗粒分别有

解得

故岩石颗粒A和B的周期之比为2：9．

（3）设地球质量为M，地球半径为r0，地球上物体的重力可视为万有引力，探测器上物体质量为m0，在地球表面重力为

G0，距土星中心r0′=3.2×105km处的引力为G0′，根据万有引力定律有

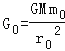
解得

故土星质量大约是地球质量的95倍．