题目内容
20. 如图所示,A是光滑绝缘固定的四分之一圆弧的端点,B是其底端,O是其圆心,OA水平,半径为R=0.8m,圆弧所在的地区域存在方向垂直纸面向里的匀强磁场,B点右侧为倾角为53°的粗糙、绝缘斜面,斜面所在区域存在水平向右的匀强电场,E=10V/m,圆弧与斜面平滑连接.质量为m=0.01kg,带电量为q=+10-2C的小球从A点同静止开始下滑,到达B点时恰好对圆弧无压力,小球与斜面的动摩擦因数为0.5,重力加速度g=10m/s2,sin53°=0.8,cos53°=0.6.求:
如图所示,A是光滑绝缘固定的四分之一圆弧的端点,B是其底端,O是其圆心,OA水平,半径为R=0.8m,圆弧所在的地区域存在方向垂直纸面向里的匀强磁场,B点右侧为倾角为53°的粗糙、绝缘斜面,斜面所在区域存在水平向右的匀强电场,E=10V/m,圆弧与斜面平滑连接.质量为m=0.01kg,带电量为q=+10-2C的小球从A点同静止开始下滑,到达B点时恰好对圆弧无压力,小球与斜面的动摩擦因数为0.5,重力加速度g=10m/s2,sin53°=0.8,cos53°=0.6.求:(1)感应强度的大小和小球在斜面上运动的最远距离;
(2)若小球在斜面最高点时撤去电场,小球第一次返回B点对圆弧的压力大小.
分析 (1)由于洛伦兹力不作功,小球从A运动到B的过程中机械能守恒,由机械能守恒定律求出小球到B时的速度.在B点,由洛伦兹力和重力的合力提供向心力,由牛顿第二定律求B.再研究小球在斜面上运动的过程,根据动能定理求小球在斜面上运动的最远距离;
(2)撤去电场后,再由动能定理求出小球返回B点时的速度大小,由牛顿运动定律求对圆弧的压力.
解答 解:(1)小球从A运动到B的过程,由机械能守恒得:
mgR=$\frac{1}{2}m{v}_{B}^{2}$,则 vB=$\sqrt{2gR}$=$\sqrt{2×10×0.8}$=4m/s
在B点,由左手定则判断可知小球所受的洛伦兹力向上,根据牛顿第二定律得:
qvBB-mg=m$\frac{{v}_{B}^{2}}{R}$
可得 B=$\frac{m(g+\frac{{v}_{B}^{2}}{R})}{q{v}_{B}}$=$\frac{0.01×(10+\frac{{4}^{2}}{0.8})}{1{0}^{-2}×4}$T=7.5T
设小球在斜面上运动的最远距离为S.
小球在斜面上运动的过程,根据动能定理得:
qEScos53°-mgSsin53°-μ(mgcos53°+qEsin53°)S=0-$\frac{1}{2}m{v}_{B}^{2}$
代入解得 S=$\frac{8}{9}$m
(2)撤去电场后,小球从最高点到返回B点的过程,由动能定理得:
mgSsin53°-μmgScos53°=$\frac{1}{2}m{v}_{B}^{′2}$,解得 vB′=$\frac{2\sqrt{3}}{3}$m/s
在B点,有N-mg-qvB′B=m$\frac{{v}_{B}^{′2}}{R}$
解得 N=(0.225+$\frac{\sqrt{3}}{20}$)N
由牛顿第三定律知,小球第一次返回B点对圆弧的压力大小N′=N=(0.225+$\frac{\sqrt{3}}{20}$)N.
答:
(1)感应强度的大小是7.5T,小球在斜面上运动的最远距离是$\frac{8}{9}$m;
(2)若小球在斜面最高点时撤去电场,小球第一次返回B点对圆弧的压力大小为(0.225+$\frac{\sqrt{3}}{20}$)N.
点评 本题是带电体在复合场中运动的问题,分析小球的受力情况,抓住每个过程和状态的规律是关键.要知道涉及高度、距离等空间量时往往首先考虑动能定理.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案| A. | 作用在运动物体上的力一定做功 | |
| B. | 功有正负之分,所以功是矢量 | |
| C. | 根据P=$\frac{W}{t}$可知,功率P与功W成正比,与时间t成反比 | |
| D. | 功率是反应做功快慢的物理量,数值上等于单位时间内做的功 |
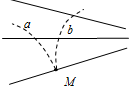 如图所示,实线为方向未知的三条电场线.a、b两个带电粒子以相同的速度从M点飞入电场,粒子仅在电场力作用下的运动轨迹如图中虚线所示,则在开始运动的一小段时间内(粒子在图示区域内)( )
如图所示,实线为方向未知的三条电场线.a、b两个带电粒子以相同的速度从M点飞入电场,粒子仅在电场力作用下的运动轨迹如图中虚线所示,则在开始运动的一小段时间内(粒子在图示区域内)( )| A. | a、b一定带异号电荷 | |
| B. | a受的电场力较大,b受的电场力较小 | |
| C. | a的速度将减小,b的速度将增大 | |
| D. | 两个粒子的电势能均减小 |
 一根轻弹簧原长8cm,劲度系数为k=50N/m,一端固定在天花板上,另一端连着小球,将小球拉离平衡位置后释放.某同学研究其中的一段运动,作出弹簧长度随时间变化的图象如图所示,重力加速度g取10m/s2,由图象可以判断( )
一根轻弹簧原长8cm,劲度系数为k=50N/m,一端固定在天花板上,另一端连着小球,将小球拉离平衡位置后释放.某同学研究其中的一段运动,作出弹簧长度随时间变化的图象如图所示,重力加速度g取10m/s2,由图象可以判断( )| A. | 小球做简谐运动的频率为4Hz,振幅为4cm | |
| B. | 小球的质量为0.1kg | |
| C. | 2s末至4s末弹力对小球做的功为零 | |
| D. | 3s末小球的加速度为10m/s2 |
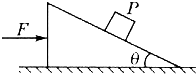 如图,质量为m的物体P放在倾角为θ的斜面体上,同时用力F向右推斜面体,使P与斜面体保持相对静止向右匀速运动,在前进水平位移为s的过程中,斜面体对P的作用力做功为( )
如图,质量为m的物体P放在倾角为θ的斜面体上,同时用力F向右推斜面体,使P与斜面体保持相对静止向右匀速运动,在前进水平位移为s的过程中,斜面体对P的作用力做功为( )| A. | F•s | B. | mgsinθ.cosθ•s | C. | mgcosθ•s | D. | 0 |
| A. | 不可能看作质点的两物体之间不存在相互作用的引力 | |
| B. | 可看作质点的两物体间的引力可用F=G$\frac{{m}_{1}{m}_{2}}{{r}^{2}}$计算 | |
| C. | 由F=G$\frac{{m}_{1}{m}_{2}}{{r}^{2}}$可知,两物体间距离r减小时,它们之间的引力增大,紧靠在一起时,万有引力非常大 | |
| D. | 引力常量的大小首先是由卡文迪许测出来的 |
 某同学做“验证机械能守恒定律”实验时不慎将一条选择好的纸带的前面一部分损坏了,剩下的一段纸带如图所示.已知打点计时器每隔时间t打一个点,重力加速度为g.这位同学对这条纸带进行了相关测量,并通过计算和比较,也得到了“重锤的机械能守恒”的结论.
某同学做“验证机械能守恒定律”实验时不慎将一条选择好的纸带的前面一部分损坏了,剩下的一段纸带如图所示.已知打点计时器每隔时间t打一个点,重力加速度为g.这位同学对这条纸带进行了相关测量,并通过计算和比较,也得到了“重锤的机械能守恒”的结论. 某同学用如图所示装置通过半径相同的A、B两球的碰撞来验证动量守恒定律,在固定斜槽时应该使斜槽末端切线水平,每次释放小球的位置应该斜槽上同一位置无初速释放,图中O点是水平槽末端在记录纸上的垂直投影点,在以下选项中,ABD是本次实验必须进行的测量?
某同学用如图所示装置通过半径相同的A、B两球的碰撞来验证动量守恒定律,在固定斜槽时应该使斜槽末端切线水平,每次释放小球的位置应该斜槽上同一位置无初速释放,图中O点是水平槽末端在记录纸上的垂直投影点,在以下选项中,ABD是本次实验必须进行的测量?