题目内容
如图所示,轨道ABCD由水平面AB、倾角为37°的斜面BC和平台CD组成,在B点平滑连接.已知AB间距离为L1,BC间距离为L2.质量为m的物体,以某一初速度从A点出发,物体与各个接触面的动摩擦因数均为μ.求: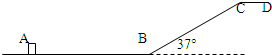
(1)物体m至少具有多大初速度值时才能冲上平台CD.
(2)若物体m刚好能运动到C点,则从B点运动到C点所需要的时间t.

(1)物体m至少具有多大初速度值时才能冲上平台CD.
(2)若物体m刚好能运动到C点,则从B点运动到C点所需要的时间t.
分析:(1)对物体受力分析,可以求得物体在AB、BC段的受力的情况,求出物体的加速度的大小,由运动学的公式可以求得物体的初速度的大小;
(2)物体从B点运动到C点时,由匀变速直线运动的规律即可求得物体运动的时间.
(2)物体从B点运动到C点时,由匀变速直线运动的规律即可求得物体运动的时间.
解答:解:设物体刚好能到达C点,在A、B、C各点的速度大小分别为V0、V1、V2,
则在AB段,由牛顿定律有:-μmg=ma1
得a1=-μg ….(1)
由公式:2a1L1=V12-V02
得V1=
….(2)
在BC段,由牛顿定律有:-μmgcosα-mgsinα-=ma2
得a2=-(0.8μ+0.6)g ….(3)
由公式:2a2L2=V22-V12 和 V2=0
得V1=
….(4)
对照(2)、(4)式得:V0=
…(5)
由公式L2=
t
得t=
,
所以物体m需要的最小初速度为V0=
,
从B点运动到C点所需要的时间t=
.
则在AB段,由牛顿定律有:-μmg=ma1
得a1=-μg ….(1)
由公式:2a1L1=V12-V02
得V1=
|
在BC段,由牛顿定律有:-μmgcosα-mgsinα-=ma2
得a2=-(0.8μ+0.6)g ….(3)
由公式:2a2L2=V22-V12 和 V2=0
得V1=
| 2(0.8μ+0.6)gL2 |
对照(2)、(4)式得:V0=
| 2μgL1+(1.6μ+1.2)gL2 |
由公式L2=
| V1+V2 |
| 2 |
得t=
2
| ||
|
所以物体m需要的最小初速度为V0=
| 2μgL1+(1.6μ+1.2)gL2 |
从B点运动到C点所需要的时间t=
2
| ||
|
点评:本题考查了牛顿第二定律和匀变速直线运动的规律,对物体受力分析,确定物体的运动的状态,在根据匀变速直线运动的规律来求解即可.

练习册系列答案
相关题目
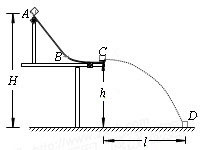
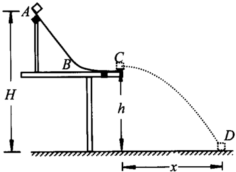 如图所示,轨道ABC被竖直地固定在水平桌面上,A距水平地面高H=0.75m,C距水平地面高h=0.45m.一质量m=0.10kg的小物块自A点从静止开始下滑,从C点以水平速度飞出后落在地面上的D点.现测得C、D两点的水平距离为x=0.60m.不计空气阻力,取g=10m/s2.求
如图所示,轨道ABC被竖直地固定在水平桌面上,A距水平地面高H=0.75m,C距水平地面高h=0.45m.一质量m=0.10kg的小物块自A点从静止开始下滑,从C点以水平速度飞出后落在地面上的D点.现测得C、D两点的水平距离为x=0.60m.不计空气阻力,取g=10m/s2.求
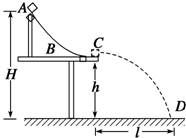 如图所示,轨道ABC被竖直地固定在水平桌面上,A距离水平地面高H=0.75m,C距离水平地面高h=0.45m.一质量m=0.10kg的小物块自A点从静止开始下滑,从C点以水平速度飞出后落在水平地面上的D点.现测得C、D两点的水平距离为l=0.60m.不计空气阻力,取g=10m/s2.求:
如图所示,轨道ABC被竖直地固定在水平桌面上,A距离水平地面高H=0.75m,C距离水平地面高h=0.45m.一质量m=0.10kg的小物块自A点从静止开始下滑,从C点以水平速度飞出后落在水平地面上的D点.现测得C、D两点的水平距离为l=0.60m.不计空气阻力,取g=10m/s2.求: 如图所示,轨道ABC的AB是半径为0.4m的光滑
如图所示,轨道ABC的AB是半径为0.4m的光滑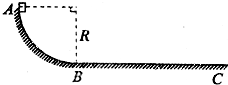 如图所示,轨道ABC的AB是半径为0.4m的光滑
如图所示,轨道ABC的AB是半径为0.4m的光滑