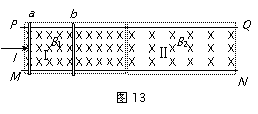Question

如图13所示，光滑、足够长、不计电阻、轨道间距为l的平行金属导轨MN、PQ，水平放在竖直向下的磁感应强度不同的两个相邻的匀强磁场中，左半部分为Ι匀强磁场区，磁感应强度为B₁；右半部分为Ⅱ匀强磁场区，磁感应强度为B₂，且B₁=2B₂。在Ι匀强磁场区的左边界垂直于导轨放置一质量为m、电阻为R₁的金属棒a，在Ι匀强磁场区的某一位置，垂直于导轨放置另一质量也为m、电阻为R₂的金属棒b。开始时b静止，给a一个向右冲量I后a、b开始运动。设运动过程中，两金属棒总是与导轨垂直。

（1）求金属棒a受到冲量后的瞬间通过金属导轨的感应电流；

（2）设金属棒b在运动到Ι匀强磁场区的右边界前已经达到最大速度，求金属棒b在Ι匀强磁场区中的最大速度值；

（3）金属棒b进入Ⅱ匀强磁场区后，金属棒b再次达到匀速运动状态，设这时金属棒a仍然在Ι匀强磁场区中。求金属棒b进入Ⅱ匀强磁场区后的运动过程中金属棒a、b中产生的总焦耳热。

 

Answer 1

（1）设金属棒a受到冲量I时的速度为v₀，金属棒a产生的感应电动势为E，金属轨道中的电流为i，则

     I=mv₀………………………………………………1分

     E=B₁lv₀………………………………………………1分

     i=………………………………………………1分

     i=………………………………………………1分

（2）金属棒a和金属棒b在左部分磁场中运动过程中所受安培力大小相等、方向相反，合力为零，故a、b组成的，水平方向动量守恒。

金属棒a和金属棒b在Ι匀强磁场区中运动过程中达到的最大速度v_m时，二金属棒速度相等，感应电流为零，二金属棒匀速运动，根据动量守恒定律有

     mv₀=2mv_m………………………………………………2分

     v_m=………………………………………………2分

（3）金属棒b进入Ⅱ匀强磁场时，设金属棒a的感应电动势为E₁，金属棒b的感应电动势为E₂，

     E₁=B₁lv_m

     E₂=B₂lv_m

     因为   B₁=2 B₂

     所以   E₁=2 E₂………………………………………………2分

    所以，金属棒b一进入Ⅱ匀强磁场，电流立即出现，在安培力作用下金属棒a做减速运动，金属棒b做加速运动。设金属棒a在Ι匀强磁场区运动速度从v_m变化到最小速度v_a，所用时间为t，金属棒b在Ⅱ匀强磁场区运动速度从v_m变化到最大速度为v_b，所用时间也为t，此后金属棒a、b都匀速运动，则

    B₁lv_a= B₂lv_b………………………………………………3分

即 v_b=2v_a………………………………………………1分

设在t时间内通过金属棒a、b的电流平均值为

根据动量定理有

B₁lt=mv_a-mv_m  方向向左………………………………………………1分

B₂lt=mv_b-mv_m  方向向右………………………………………………1分

解得：………………………………………………1分

      ………………………………………………1分

设金属棒b进入Ⅱ匀强磁场后，金属棒a、b产生的总焦耳热为Q，根据能量守恒，有

……………………………………1分

Q=……………………………………1分