题目内容
如图所示,由六根质量不计的导体棒组成一个人字形线圈,放在光滑绝缘水平面上,每根导棒长均为L=1m,线圈总电阻R=0.2Ω,将ad与a/d/用细线OO/拉住,e、f是两个质量都为m=0.1kg光滑转轴,四根倾斜导体棒与水平面成37 0角。人字形线圈在水平面投影区内有两块对称的区域,竖直向上的匀强磁场B穿过这两块区域。如图中阴影区域所示(ad与a/d/恰在磁场中),其他地方没有磁场。磁场按B= +0.5t 的规律变化,取sin37°=0.6,cos37°=0.8。求:
+0.5t 的规律变化,取sin37°=0.6,cos37°=0.8。求:
(1)t=0时水平面对线圈ad边支持力的大小和此时通过线圈电流大小;
(2)经过多少时间线圈的ad边与a/d/边开始运动?
(3)若在磁场力作用下经过一段时间,当线圈中产生了Q=1.2J热量后线圈刚好能完全直立(即ad边与a/d/边并拢在一起),则在此过程中磁场对线圈总共提供了多少能量?
(4)若人形线圈从直立状态又散开,此时磁感强度为B0 = T且不再变化,则ad边与a/d/再次刚进入磁场时,通过线圈的电流为多大?
T且不再变化,则ad边与a/d/再次刚进入磁场时,通过线圈的电流为多大?
 +0.5t 的规律变化,取sin37°=0.6,cos37°=0.8。求:
+0.5t 的规律变化,取sin37°=0.6,cos37°=0.8。求: (1)t=0时水平面对线圈ad边支持力的大小和此时通过线圈电流大小;
(2)经过多少时间线圈的ad边与a/d/边开始运动?
(3)若在磁场力作用下经过一段时间,当线圈中产生了Q=1.2J热量后线圈刚好能完全直立(即ad边与a/d/边并拢在一起),则在此过程中磁场对线圈总共提供了多少能量?
(4)若人形线圈从直立状态又散开,此时磁感强度为B0 =
 T且不再变化,则ad边与a/d/再次刚进入磁场时,通过线圈的电流为多大?
T且不再变化,则ad边与a/d/再次刚进入磁场时,通过线圈的电流为多大?
(1)1A;(2)2s;(3)2J;(4)8.9A。
(14分)
(1)对整个线圈以a/d/为转动轴,由力矩平衡有
N×2Lcos37o =2mg×Lcos37o
由上式得 N=mg=0.1×10N=1N (1分)
 V (1分)
V (1分)
 A (1分)
A (1分)
(2)平衡刚被破坏时细线OO/中拉力为零,对半个线圈以e f为转动轴,由力矩平衡有
FA×Lsin37o ="N×L" cos37o 求得 (1分)
(1分)
由 (1分)
(1分)
得 (1分)
(1分)
由关系式Bt= +0.5t 得
+0.5t 得 (1分)
(1分)
(3)线圈由平衡被破坏到完全直立过程中机械能的增加量
ΔEP=2mgL(1-sin37o)=2×0.1×10×1×(1-0.6)J=0.8J (1分)
磁场提供的能量 E=ΔEP+Q=(0.8+1.2)J=2J (1分)
(4)人形线圈从直立状态又散开,ad边与a/d/再次刚进入磁场时,设两轴e、f的速度为v(方向竖直向下),ad边与a/d/边的速度大小为vx (方向水平)
由动能定理 2mgL(1-cos37o)=2× mv2 (1分)
mv2 (1分)
 (1分)
(1分)
而vx =vctg37o=2× =
= m/s (1分)
m/s (1分)
ad边与a/d/边每一条边的电动势Eˊ=B0Lvx = V (1分)
V (1分)
线圈中的电流 Iˊ=
 (1分)
(1分)
(1)对整个线圈以a/d/为转动轴,由力矩平衡有
N×2Lcos37o =2mg×Lcos37o
由上式得 N=mg=0.1×10N=1N (1分)
 V (1分)
V (1分) A (1分)
A (1分)(2)平衡刚被破坏时细线OO/中拉力为零,对半个线圈以e f为转动轴,由力矩平衡有
FA×Lsin37o ="N×L" cos37o 求得
 (1分)
(1分)由
 (1分)
(1分)得
 (1分)
(1分)由关系式Bt=
 +0.5t 得
+0.5t 得 (1分)
(1分)(3)线圈由平衡被破坏到完全直立过程中机械能的增加量
ΔEP=2mgL(1-sin37o)=2×0.1×10×1×(1-0.6)J=0.8J (1分)
磁场提供的能量 E=ΔEP+Q=(0.8+1.2)J=2J (1分)
(4)人形线圈从直立状态又散开,ad边与a/d/再次刚进入磁场时,设两轴e、f的速度为v(方向竖直向下),ad边与a/d/边的速度大小为vx (方向水平)
由动能定理 2mgL(1-cos37o)=2×
 mv2 (1分)
mv2 (1分) (1分)
(1分)而vx =vctg37o=2×
 =
= m/s (1分)
m/s (1分)ad边与a/d/边每一条边的电动势Eˊ=B0Lvx =
 V (1分)
V (1分)线圈中的电流 Iˊ=

 (1分)
(1分)
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目



 。横梁下边缘离地面的高度为h,足球质量为m,运动员对足球做的功为W1,足球运动过程中克服空气阻力做功为W2,选地面为零势能面,下列说法正确的是
。横梁下边缘离地面的高度为h,足球质量为m,运动员对足球做的功为W1,足球运动过程中克服空气阻力做功为W2,选地面为零势能面,下列说法正确的是
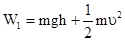 W
W

