题目内容
16.某物体做匀减速直线运动3m末停下,它通过第1m,第2m,第3m所用的时间比为($\sqrt{3}$-$\sqrt{2}$):($\sqrt{2}$-1):1,通过前1m,前2m,前3m所用时间之比为($\sqrt{3}$-$\sqrt{2}$):($\sqrt{3}$-1):$\sqrt{3}$,通过前1m,前2m,前3m的平均速度之比为2($\sqrt{3}$+$\sqrt{2}$):($\sqrt{3}$+1):2$\sqrt{3}$;.分析 将匀减速直线运动反向看作初速度为零的匀加速直线运动;根据相临相等的位移内的时间之比结论反向得出时间之比;再根据题意明确前1m,前2m,前3m所用时间之比;再根据平均速度公式可求得平均速度.
解答 解:对于末速度为零的匀减速直线运动,可以逆向看作初速度为零的匀加速直线运动;
则对于初速度为零的匀加速直线运动,在相邻相等的位移内所用时间之比为:
因此对于匀减速直线运动,通过第1m,第2m,第3m所用的时间比为($\sqrt{3}$-$\sqrt{2}$):($\sqrt{2}$-1):1;
故前1m,前2m,前3m所用时间之比为:($\sqrt{3}$-$\sqrt{2}$):($\sqrt{3}$-1):$\sqrt{3}$
平均速度$\overline{v}$=$\frac{x}{t}$;故$\frac{1}{\sqrt{3}-\sqrt{2}}$:$\frac{1}{\sqrt{3}-1}$:$\sqrt{3}$=2($\sqrt{3}$+$\sqrt{2}$):($\sqrt{3}$+1):2$\sqrt{3}$;
故答案为:($\sqrt{3}$-$\sqrt{2}$):($\sqrt{2}$-1):1;($\sqrt{3}$-$\sqrt{2}$):($\sqrt{3}$-1):$\sqrt{3}$;2($\sqrt{3}$+$\sqrt{2}$):($\sqrt{3}$+1):2$\sqrt{3}$;
点评 本题考查匀变速直线运动的基本结论的综合应用,要注意明确逆向思维及初速度为零的匀变速直线运动结论的正确应用.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
6. 比功率是衡量汽车动力性能的一个综合指标,具体是指汽车发动机最大功率与汽车总质量之比,一般来讲,对同类型汽车而言,比功率越大,汽车的动力性越好,普通国产抵挡车大概范围在0.04-0.07kW/kg,中档车的大概范围从0.06-0.10 kW/kg,高档车则更高,范围也更广,大概范围从0.08-0.13kW/kg,为爱了粗略检测一种新汽车的比功率,工程师用速度传感器记录下该汽车在水平道路上,以恒定最大功率从静止开始启动到最大速度过程中的速度图象如图所示,已知从静止开始以恒定功率启动后26s,到达机车的最大速度40m/s,汽车运动过程中阻力不变,则根据比功率来粗略可以判断( )
比功率是衡量汽车动力性能的一个综合指标,具体是指汽车发动机最大功率与汽车总质量之比,一般来讲,对同类型汽车而言,比功率越大,汽车的动力性越好,普通国产抵挡车大概范围在0.04-0.07kW/kg,中档车的大概范围从0.06-0.10 kW/kg,高档车则更高,范围也更广,大概范围从0.08-0.13kW/kg,为爱了粗略检测一种新汽车的比功率,工程师用速度传感器记录下该汽车在水平道路上,以恒定最大功率从静止开始启动到最大速度过程中的速度图象如图所示,已知从静止开始以恒定功率启动后26s,到达机车的最大速度40m/s,汽车运动过程中阻力不变,则根据比功率来粗略可以判断( )
 比功率是衡量汽车动力性能的一个综合指标,具体是指汽车发动机最大功率与汽车总质量之比,一般来讲,对同类型汽车而言,比功率越大,汽车的动力性越好,普通国产抵挡车大概范围在0.04-0.07kW/kg,中档车的大概范围从0.06-0.10 kW/kg,高档车则更高,范围也更广,大概范围从0.08-0.13kW/kg,为爱了粗略检测一种新汽车的比功率,工程师用速度传感器记录下该汽车在水平道路上,以恒定最大功率从静止开始启动到最大速度过程中的速度图象如图所示,已知从静止开始以恒定功率启动后26s,到达机车的最大速度40m/s,汽车运动过程中阻力不变,则根据比功率来粗略可以判断( )
比功率是衡量汽车动力性能的一个综合指标,具体是指汽车发动机最大功率与汽车总质量之比,一般来讲,对同类型汽车而言,比功率越大,汽车的动力性越好,普通国产抵挡车大概范围在0.04-0.07kW/kg,中档车的大概范围从0.06-0.10 kW/kg,高档车则更高,范围也更广,大概范围从0.08-0.13kW/kg,为爱了粗略检测一种新汽车的比功率,工程师用速度传感器记录下该汽车在水平道路上,以恒定最大功率从静止开始启动到最大速度过程中的速度图象如图所示,已知从静止开始以恒定功率启动后26s,到达机车的最大速度40m/s,汽车运动过程中阻力不变,则根据比功率来粗略可以判断( )| A. | 这种车可能是国产高档车 | B. | 这种车可能是国产中档车 | ||
| C. | 这种车可能是国产低档车 | D. | 条件不足,不能判断 |
 如图所示,在平面坐标XOY内有垂直纸面向外的匀强磁场,A、B两点分别在Y轴上和X轴上,到原点O的距离分别为a和$\sqrt{3}$a,一正粒子以大小为V0的初速度从原点O出发恰好能经过A点和B点,已知正粒子的质量为m,电荷量为q,不计粒子的重力,求:
如图所示,在平面坐标XOY内有垂直纸面向外的匀强磁场,A、B两点分别在Y轴上和X轴上,到原点O的距离分别为a和$\sqrt{3}$a,一正粒子以大小为V0的初速度从原点O出发恰好能经过A点和B点,已知正粒子的质量为m,电荷量为q,不计粒子的重力,求: 某同学在探究物体做曲线运动的条件时,将一条形磁铁放在水平桌面的不同位置,让小钢球在水平桌面上从同一位置过以相同初速度v运动,得到不同的运动轨迹.磁铁放在位置A时,小钢球的运动轨迹是b(填轨迹的字母代号),磁铁放在位置B时,小钢球的运动轨迹是c(填轨迹的字母代号),实验表明,当物体所受合外力的方向跟物体的运动方向不在(选填“在”或“不在”)同一直线上时,物体做曲线运动.
某同学在探究物体做曲线运动的条件时,将一条形磁铁放在水平桌面的不同位置,让小钢球在水平桌面上从同一位置过以相同初速度v运动,得到不同的运动轨迹.磁铁放在位置A时,小钢球的运动轨迹是b(填轨迹的字母代号),磁铁放在位置B时,小钢球的运动轨迹是c(填轨迹的字母代号),实验表明,当物体所受合外力的方向跟物体的运动方向不在(选填“在”或“不在”)同一直线上时,物体做曲线运动.
 如图是一列简谐波在t=0时刻的波形图,介质中x=4m处质点沿y轴方向做简谐运动的表达式为y=0.2sin5πtcm.关于这列波,下列说法正确的是ABE.
如图是一列简谐波在t=0时刻的波形图,介质中x=4m处质点沿y轴方向做简谐运动的表达式为y=0.2sin5πtcm.关于这列波,下列说法正确的是ABE. 如图所示,有一块木板静止在足够长的粗糙水平面上,木板质量为M=4kg,长为L=1.4m,木板右端放着一小滑块,小滑块质量为m=1kg,可视为质点,小滑块与木板之间的动摩擦因数为μ1=0.4,木板与地面之间的动摩擦因数为μ2=0.1,取g=10m/s2.
如图所示,有一块木板静止在足够长的粗糙水平面上,木板质量为M=4kg,长为L=1.4m,木板右端放着一小滑块,小滑块质量为m=1kg,可视为质点,小滑块与木板之间的动摩擦因数为μ1=0.4,木板与地面之间的动摩擦因数为μ2=0.1,取g=10m/s2.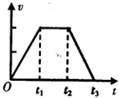 起重机将重物由地面竖直吊到空中某个高度,这一过程的v-t图象如图所示,下列能反映钢索拉力的功率随时间变化的图象是( )
起重机将重物由地面竖直吊到空中某个高度,这一过程的v-t图象如图所示,下列能反映钢索拉力的功率随时间变化的图象是( )



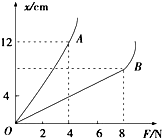 为了探究弹簧弹力F和弹簧伸长量x的关系,某同学选了A、B两根规格不同的弹簧进行测试,根据测得的数据绘出如图所示的图象,从图象上看,该同学没能完全按实验要求做,使图象上端成为曲线,图象上端成为曲线的原因是超出弹性限度.弹簧A的劲度系数为$\frac{100}{3}$(可用分数表示).若要制作一个精确度较高的弹簧秤,应选弹簧A(填“A”或“B”).
为了探究弹簧弹力F和弹簧伸长量x的关系,某同学选了A、B两根规格不同的弹簧进行测试,根据测得的数据绘出如图所示的图象,从图象上看,该同学没能完全按实验要求做,使图象上端成为曲线,图象上端成为曲线的原因是超出弹性限度.弹簧A的劲度系数为$\frac{100}{3}$(可用分数表示).若要制作一个精确度较高的弹簧秤,应选弹簧A(填“A”或“B”).