题目内容
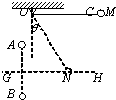
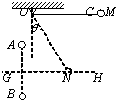 如图所示,处于同一条竖直线上的两个固定点电荷A、B带等量同种正电荷,电荷量均为Q,GH是它们连线的垂直平分线,另有一个带电小球C,质量为m、电荷量为+q(可视为点电荷),被长为L的绝缘轻质细线悬挂于O点,现在把小球C拉到M点,使细线水平绷直且与A、B处于同一竖直平面内,由静止开始释放C,小球向下运动到GH线上的N点时速度刚好为零.此时细线与竖直方向的夹角θ=30°,N与A、B恰好构成一边长为a的正三角形.已知静电力恒量为k,求:
如图所示,处于同一条竖直线上的两个固定点电荷A、B带等量同种正电荷,电荷量均为Q,GH是它们连线的垂直平分线,另有一个带电小球C,质量为m、电荷量为+q(可视为点电荷),被长为L的绝缘轻质细线悬挂于O点,现在把小球C拉到M点,使细线水平绷直且与A、B处于同一竖直平面内,由静止开始释放C,小球向下运动到GH线上的N点时速度刚好为零.此时细线与竖直方向的夹角θ=30°,N与A、B恰好构成一边长为a的正三角形.已知静电力恒量为k,求:(1)在点电荷A、B所形成的电场中,M、N两点的电势差;
(2)小球运动到N点瞬间,细线对小球的拉力F.
分析:(1)小球从M运动到N的过程中,重力做正功,电场力做负功,电场力做功为qUMN,根据动能定理求解M、N两点的电势差;
(2)小球到达N点时速度为零,圆周运动的向心力为零,即小球在N点沿细线方向合力为零,由此即可列式求解细线对小球的拉力F.
(2)小球到达N点时速度为零,圆周运动的向心力为零,即小球在N点沿细线方向合力为零,由此即可列式求解细线对小球的拉力F.
解答:解:(1)小球从M点运动到N点的过程中,根据动能定理得
qUMN+mgLcos30°=0
得M、N两点的电势差UMN=-
mgL
(2)由题意,小球到达N点时速度为零,圆周运动的向心力为零,则小球在N点沿细线方向合力为零,则有
F-mgcos30°-k
cos30°=0
所以F=
(mg+
)
答:(1)在点电荷A、B所形成的电场中,M、N两点的电势差是-
mgL;
(2)小球运动到N点瞬间,细线对小球的拉力F是
(mg+
).
qUMN+mgLcos30°=0
得M、N两点的电势差UMN=-
| ||
| 2 |
(2)由题意,小球到达N点时速度为零,圆周运动的向心力为零,则小球在N点沿细线方向合力为零,则有
F-mgcos30°-k
| a2 |
所以F=
| ||
| 2 |
| kQq |
| a2 |
答:(1)在点电荷A、B所形成的电场中,M、N两点的电势差是-
| ||
| 2 |
(2)小球运动到N点瞬间,细线对小球的拉力F是
| ||
| 2 |
| kQq |
| a2 |
点评:本题考查电场中力与能的性质,要注意小球在拉力、重力及库仑力的作用下做圆周运动,故应明确合力充当了向心力.

练习册系列答案
相关题目
 如图所示,处于同一条竖直线上的两个点电荷A、B带等量同种电荷,电荷量为Q; G、H是它们连线的垂直平分线.另有一个带电小球C,质量为m、电荷量为+q(可视为点电荷),被长为L的绝缘轻细线悬挂于O点,现在把小球C拉起到M点,使细线水平且与A、B处于同一竖直面内,由静止开始释放,小球C向下运动到GH线上的N点时刚好速度为零,此时细线与竖直方向上的夹角θ=30°则下列说法正确的是( )
如图所示,处于同一条竖直线上的两个点电荷A、B带等量同种电荷,电荷量为Q; G、H是它们连线的垂直平分线.另有一个带电小球C,质量为m、电荷量为+q(可视为点电荷),被长为L的绝缘轻细线悬挂于O点,现在把小球C拉起到M点,使细线水平且与A、B处于同一竖直面内,由静止开始释放,小球C向下运动到GH线上的N点时刚好速度为零,此时细线与竖直方向上的夹角θ=30°则下列说法正确的是( )