题目内容
3.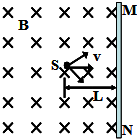 电子源S能在图所示平面360°范围内发射速率相同、质量为m、电荷量为e的电子,MN是足够大的竖直挡板,S离挡板水平距离L=16cm,挡板左侧充满垂直于纸面向里的匀强磁场,磁感应强度B=5.0×10-4T,电子速度大小为v=1.0×107m/s,方向可变(只在纸面内变化),电子的比荷e/m=2.0×1011C/kg,求电子打中竖直挡板的区域长度.(已知sin53°=0.8,cos53°=0.6)
电子源S能在图所示平面360°范围内发射速率相同、质量为m、电荷量为e的电子,MN是足够大的竖直挡板,S离挡板水平距离L=16cm,挡板左侧充满垂直于纸面向里的匀强磁场,磁感应强度B=5.0×10-4T,电子速度大小为v=1.0×107m/s,方向可变(只在纸面内变化),电子的比荷e/m=2.0×1011C/kg,求电子打中竖直挡板的区域长度.(已知sin53°=0.8,cos53°=0.6)
分析 电子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律求出电子的轨道半径,作出电子的运动轨迹,然后确定电子打中竖直板区域的长度.
解答 解:电子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:
evB=m$\frac{{v}^{2}}{r}$,
解得:r=0.1m=10cm,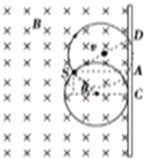
粒子速度方向与轨迹的弯曲方向的关系如图.
打在最上端的轨迹与挡板的交点到S的距离恰好是直径,打在最下端的轨迹与挡板相切.由几何知识得:
AD=$\sqrt{(2R)^{2}-{L}^{2}}$=$\sqrt{(2×10)^{2}-1{6}^{2}}$=12cm,
r+rcosθ=L,cosθ=0.6,
则θ=53°,
AC=rsian53°=10×0.8=8cm,
电子打中挡板区域的长度:l=AD+AC=20cm;
答:电子打中竖直挡板的区域长度为20cm.
点评 本题是带电粒子在磁场场中运动的问题,带电粒子在磁场中做匀速圆周运动,要求同学们能画出粒子运动的轨迹,灵活运用几何知识求出轨迹半径或范围.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.如图,正弦交变电流的说法不正确是( )


| A. | 电流的峰值为0.6$\sqrt{2}$ A | B. | 电流的有效值为0.6 A | ||
| C. | 电流的周期为2 S | D. | 电流的频率为50HZ |
11.下列关于使用打点计时器的说法,其中正确的是( )
| A. | 不要在未放纸带时通电打点,每次打点完毕,应及时切断电源,切忌长时间通电使用 | |
| B. | 若发现振片振幅不稳定,应调节振片螺母,以使振动稳定 | |
| C. | 若打出的点带尾巴或双点,则是由于打点针太长所造成的,应适当调节打点针的长度 | |
| D. | 若打的点不清楚或有漏点,则检查复写纸是否已损坏或是否打点针太短 |
18.关于回旋加速器中,下列说法正确的是( )
| A. | 电场和磁场同时用来加速带电粒子 | |
| B. | 回旋加速器的半径越大,同一带电粒子获得的动能越大,与匀强磁场的磁感应强度无关 | |
| C. | 同一带电粒子获得的最大动能只与交流电压的电源有关,而与交流电源的频率无关 | |
| D. | 电场用来加速带电粒子,磁场则使带电粒子旋转 |
 如图所示,甲图中物体A从高H处由静止开始下落.乙图中物体B与C通过光滑轻滑轮用细绳相连,C放在光滑水平桌面上,C的质量是B的一半,物体B也从H高处由静止下落.求这两种情况下,A、B离地面的高度h为多少时,其动能等于势能?(设C尚未离开桌面)
如图所示,甲图中物体A从高H处由静止开始下落.乙图中物体B与C通过光滑轻滑轮用细绳相连,C放在光滑水平桌面上,C的质量是B的一半,物体B也从H高处由静止下落.求这两种情况下,A、B离地面的高度h为多少时,其动能等于势能?(设C尚未离开桌面) 矩形导线框abcd置于竖直向上的磁感应强度为B的匀强磁场中,其中ab、cd边长度相等均为L,且ab、cd边质量均忽略不计,bc边长度为d,质量为m,线框可绕MN转动,导线框中通以MabcdN方向的恒定电流后,导线框往纸外偏转角θ而达到平衡.求:
矩形导线框abcd置于竖直向上的磁感应强度为B的匀强磁场中,其中ab、cd边长度相等均为L,且ab、cd边质量均忽略不计,bc边长度为d,质量为m,线框可绕MN转动,导线框中通以MabcdN方向的恒定电流后,导线框往纸外偏转角θ而达到平衡.求:
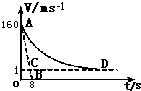 “神舟”五号飞船完成了预定空间科学和技术试验任务后,返回舱开始从太空向地球表面按预定轨道返回.返回舱开始时通过自身制动发动机进行调控变速下降,穿越大气层后,在一定的高度打开阻力降落伞进一步减速下降.这一过程中若返回舱所受空气阻力与速度的平方成正比,比例系数(空气阻力系数)为k,所受空气浮力恒定不变,且认为竖直降落,从某时刻开始计时,返回舱的运动v-t图象如图中的AD曲线所示.图中AB是曲线AD在A点的切线,切线交于横轴一点B,其坐标为(8,0),CD是曲线AD的渐近线.假如返回舱总质量M=400kg,g取10m/s2.试问:
“神舟”五号飞船完成了预定空间科学和技术试验任务后,返回舱开始从太空向地球表面按预定轨道返回.返回舱开始时通过自身制动发动机进行调控变速下降,穿越大气层后,在一定的高度打开阻力降落伞进一步减速下降.这一过程中若返回舱所受空气阻力与速度的平方成正比,比例系数(空气阻力系数)为k,所受空气浮力恒定不变,且认为竖直降落,从某时刻开始计时,返回舱的运动v-t图象如图中的AD曲线所示.图中AB是曲线AD在A点的切线,切线交于横轴一点B,其坐标为(8,0),CD是曲线AD的渐近线.假如返回舱总质量M=400kg,g取10m/s2.试问: