Question

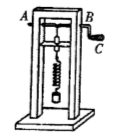
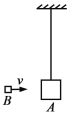
【题目】如图，物块A通过一不可伸长的轻绳悬挂在天花板下，初始时静止；从发射器（图中未画出）射出的物块B沿水平方向与A相撞，碰撞后两者粘连在一起运动；碰撞前B的速度的大小v及碰撞后A和B一起上升的高度h均可由传感器（图中未画出）测得。某同学以h为纵坐标，v2为横坐标，利用实验数据作直线拟合，求得该直线的斜率为k=1.92 ×10-3 s2/m。已知物块A和B的质量分别为mA=0.400 kg和mB=0.100 kg，重力加速度大小g=9.80 m/s2。

（i）若碰撞时间极短且忽略空气阻力，求h–v2直线斜率的理论值k0；

（ii）求k值的相对误差δ（δ=×100%，结果保留1位有效数字）。

Answer 1

【答案】（i）2.04×10–3 s2/m （ii）6%

【解析】（i）设物块A和B碰撞后共同运动的速度为v'，由动量守恒定律有

mBv=（mA+mB）v' ①

在碰后A和B共同上升的过程中，由机械能守恒定律有

②

联立①②式得③

由题意得④

代入题给数据得k0=2.04×10–3 s2/m⑤

（ii）按照定义δ=×100%⑥

由⑤⑥式和题给条件得δ=6%⑦