题目内容
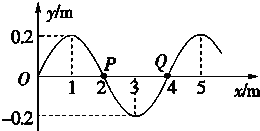一列简谐横波沿x轴负向传播，t=0时刻的波形如图，介质中质点P、Q分别位于x=2m、x=4m处．从t=0时刻开始计时，当t=26s时质点Q第4次到达波峰．（1）求波速．
（2）写出质点P做简谐运动的表达式（不要求推导过程）．
分析：（1）根据波形图得到波长；从t=0时刻开始计时，当t=26s时质点Q刚好第4次到达波峰，判断出周期；然后根据v=
计算波速；
（2）根据波形图得到振幅A，然后根据公式y=Asinωt列式求解．
| λ |
| T |
（2）根据波形图得到振幅A，然后根据公式y=Asinωt列式求解．
解答：解：①根据波形图得到波长λ=4m；
t=0时刻，质点Q正向上运动；从t=0时刻开始计时，当t=26s时质点Q刚好第4次到达波峰，故有
3T+
T=t
解得：T=
=
=8s
故波速为：v=
=
=0.5m/s；
②t=0时刻，质点P正在向下运动，振幅为：A=0.2m；
角频率为：ω=
=
=
rad/s
故质点P做简谐运动的表达式为：y=0.2sin（
t+π）m；
答：（1）波速为1m/s；
（2）点P做简谐运动的表达式为y=0.2sin（
t+π）m．
t=0时刻，质点Q正向上运动；从t=0时刻开始计时，当t=26s时质点Q刚好第4次到达波峰，故有
3T+
| 1 |
| 4 |
解得：T=
| 4t |
| 13 |
| 4×26 |
| 13 |
故波速为：v=
| λ |
| T |
| 4 |
| 8 |
②t=0时刻，质点P正在向下运动，振幅为：A=0.2m；
角频率为：ω=
| 2π |
| T |
| 2π |
| 8 |
| π |
| 8 |
故质点P做简谐运动的表达式为：y=0.2sin（
| π |
| 4 |
答：（1）波速为1m/s；
（2）点P做简谐运动的表达式为y=0.2sin（
| π |
| 4 |
点评：本题综合考查了质点的振动和波动，关键是要能从波速方向判断出质点的振动方向，同时要能从图象得到波长并进一步求解波速．
练习册系列答案
开心练习课课练与单元检测系列答案
开心试卷期末冲刺100分系列答案
双基同步导航训练系列答案
相关题目
（2008?虹口区二模）如图所示，一列简谐横波沿x轴负方向传播，振幅A=4cm．在t=0时刻，平衡位置相距5cm的两质点a、b的位移分别是2cm、-2cm，它们的运动方向都沿y轴的负方向，据此可以推断（ ）
