题目内容
在水平地面上竖直固定一根内壁光滑的圆管，管的半径R=3.6m（管的内径大小可以忽略），管的出口A在圆心的正上方，入口B与圆心的连线与竖直方向成60°角，如图所示．现有一只质量m=1kg的小球（可视为质点）从某点P以一定的初速度水平抛出，恰好从管口B处沿切线方向飞入，小球到达A时恰好与管壁无作用力．取g=10m/s2．求：
（1）小球到达圆管最高点A时的速度大小；
（2）小球在管的最低点C时，管壁对小球的弹力大小；
（3）小球抛出点P到管口B的水平距离x．
【答案】
（1）
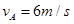（2）
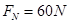，方向竖直向上（3）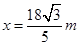
【解析】
试题分析：（1）小球在最高点时，对管壁无作用力，根据向心力公式可得：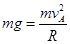
可得小球到达圆管最高点时的速度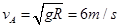
（2）设最低点C的速度为v，小球从管的最低点到最高点A，有机械能守恒定律可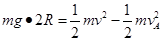得：
,解得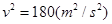
在最低点，由向心力公式可得：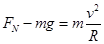
可得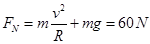
，方向竖直向上
（3）设B点的速度为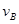
，由机械能守恒定律 可得：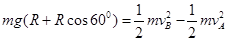
解得：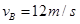
由平抛运动规律可知，小球做平抛运动过程的初速度
，
在B点的竖直速度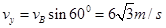
，根据
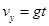可得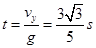
根据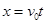
可知：小球的抛出点到管口B的水平距离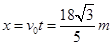
考点：考查了圆周运动，机械能守恒定律等综合应用，中档偏高
练习册系列答案
相关题目
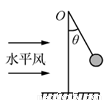
（2013?南通二模）气象研究小组用图示简易装置测定水平风速．在水平地面上竖直固定一直杆，半径为R、质量为m的薄空心塑料球用细线悬于杆顶端O，当水平风吹来时，球在风力的作用下飘起来．已知风力大小正比于风速和球正对风的截面积，当风速v0=3m/s时，测得球平衡时细线与竖直方向的夹角θ=30°．则（ ）
（2013?南京模拟）在水平地面上竖直固定一根内壁光滑的圆管，管的半径R=3.6m（管的内径大小可以忽略），管的出口A在圆心的正上方，入口B与圆心的连线与竖直方向成60°角，如图所示．现有一只质量m=1kg的小球（可视为质点）从某点P以一定的初速度水平抛出，恰好从管口B处沿切线方向飞入，小球到达A时恰好与管壁无作用力．取g=10m/s2．求：
