题目内容
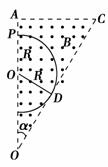
如图8-2-9所示,直角三角形OAC(α=30°)区域内有B=0.5 T的匀强磁场,方向如图所示.两平行极板M,N接在电压为U的直流电源上,左板为高电势.一带正电的粒子从靠近M板由静止开始加速,从N板的小孔射出电场后,垂直OA的方向从P点进入磁场中.带电粒子的比荷为![]() =105C/kg,OP间距离为L=0.3 m.全过程不计粒子所受的重力,则:
=105C/kg,OP间距离为L=0.3 m.全过程不计粒子所受的重力,则:
(1)若加速电压U=120 V,通过计算说明粒子从三角形OAC的哪一边离开磁场?
(2)求粒子分别从OA、OC边离开磁场时粒子在磁场中运动的时间.

图8-2-9
解析 (1)如图所示,当带电粒子的轨迹与OC边相切时为临界状态,设临界半径为R,加速电压U0,则有:
R+![]() =L,解得R=0.1 m,qU0=
=L,解得R=0.1 m,qU0=![]() mv2,qvB=m
mv2,qvB=m![]() ,U0=125 V,U<U0,则r<R,粒子从OA边射出.
,U0=125 V,U<U0,则r<R,粒子从OA边射出.
(2)带电粒子在磁场做圆周运动的周期为T=![]() =4π×10-5s
=4π×10-5s
当粒子从OA边射出时,粒子在磁场中恰好运动了半个周期
t1=![]() =2π×10-5s
=2π×10-5s
当粒子从OC边射出时,粒子在磁场中运动的时间小于![]() 周期,
周期,
即t2≤![]() =
=![]() ×10-5s.(双直线边界模型)
×10-5s.(双直线边界模型)
答案 (1)OA边 (2)2π×10-5s 小于等于![]() ×10-5s
×10-5s

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目