题目内容
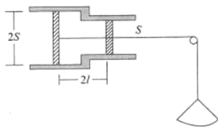
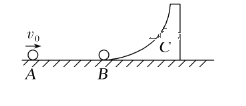
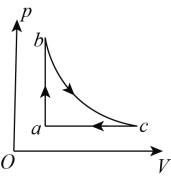
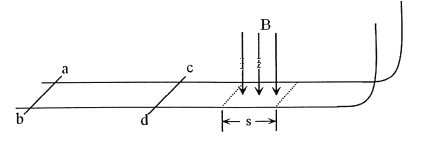
【题目】如图所示,有两根足够长的平行光滑导轨水平放置,右侧用一小段光滑圆弧和另一对竖直光滑导轨平滑连接,导轨间距L=1m。细金属棒ab和cd垂直于导轨静止放置,它们的质量m均为1kg,电阻R均为0.5Ω。cd棒右侧lm处有一垂直于导轨平面向下的矩形匀强磁场区域,磁感应强度B=1T,磁场区域长为s。以cd棒的初始位置为原点,向右为正方向建立坐标系。现用向右的水平恒力F=1.5N作用于ab棒上,作用4s后撤去F。撤去F之后ab棒与cd棒发生弹性碰撞,cd棒向右运动。金属棒与导轨始终接触良好,导轨电阻不计,空气阻力不计。(g=10m/s2)求:
(1) ab棒与cd棒碰撞后瞬间的速度分别为多少;
(2)若s=1m,求cd棒滑上右侧竖直导轨,距离水平导轨的最大高度h;
(3)若可以通过调节磁场右边界的位置来改变s的大小,写出cd棒最后静止时与磁场左边界的距离x的关系。(不用写计算过程)
【答案】(1)0,![]() ;(2)1.25 m;(3)见解析
;(2)1.25 m;(3)见解析
【解析】
(1)对ab棒,由动量定理得
![]()
ab棒与cd棒碰撞过程,取向右方向为正,对系统由动量守恒定律得
![]()
由系统机械能守恒定律得
![]()
解得![]() ,
,![]()
(2)由安培力公式可得![]()
对cd棒进入磁场过程,由动量定理得
![]()
设导体棒cd进出磁场时回路磁通量变化量为
![]()
![]()
以上几式联立可得![]() 。
。
对cd棒出磁场后由机械能守恒定律可得
![]()
联立以上各式得![]() 。
。
(3)第一种情况如果磁场s足够大,cd棒在磁场中运动距离![]() 时速度减为零,由动量定理可得
时速度减为零,由动量定理可得
![]()
设磁通量变化量为![]()
![]()
流过回路的电量
![]()
联立可得![]()
即s≥6 m,x=6 m,停在磁场左边界右侧6m处。
第二种情况cd棒回到磁场左边界仍有速度,这时会与ab再次发生弹性碰撞,由前面计算可得二者速度交换,cd会停在距磁场左边界左侧1m处,设此种情况下磁场区域宽度![]() ,向右运动时有
,向右运动时有
![]()
返回向左运动时
![]()
通过回路的电量
![]()
联立可得![]()
即s<3 m时,x=1 m,停在磁场左边界左侧1m处;
第三种情况3 m≤s<6 m,
向右运动时有
![]()
通过回路的电量
![]()
返回向左运动时
![]()
通过回路的电量
![]()
联立可得x=(2s-6)m,在磁场左边界右侧。

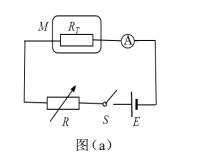
【题目】某实验小组利用如图(a)所示的电路探究在25![]() ~80
~80![]() 范围内某热敏电阻的温度特性。所用器材有:一热敏电阻RT放在控温容器M内;A为电流表,量程Im为6mA,内阻r为10Ω;E为直流电源,电动势E为3V,内阻忽略不计;R为电阻箱,最大阻值为999.9Ω,S为开关。
范围内某热敏电阻的温度特性。所用器材有:一热敏电阻RT放在控温容器M内;A为电流表,量程Im为6mA,内阻r为10Ω;E为直流电源,电动势E为3V,内阻忽略不计;R为电阻箱,最大阻值为999.9Ω,S为开关。
实验时,先按图(a)连接好电路。再将温控室的温度t升至80.0![]() ,将开关S接通,调节R,使电流表读数半偏,记下此时R的读数。逐步降低温控室的温度t,调节R,使电流表读数半偏,得到相应温度下R的阻值,直至温度降到25.0
,将开关S接通,调节R,使电流表读数半偏,记下此时R的读数。逐步降低温控室的温度t,调节R,使电流表读数半偏,得到相应温度下R的阻值,直至温度降到25.0![]() 。实验得到的R-t数据见下表。
。实验得到的R-t数据见下表。
t/℃ | 25.0 | 30.0 | 40.0 | 50.0 | 60.0 | 70.0 | 80.0 |
R/Ω | 90.0 | 310.0 | 490.0 | 600.0 | 670.0 | 720.0 | 750.0 |
回答下列问题:
(1)在闭合S前,图中R的阻值应调到_________(填“最大”或“最小”);
(2)写出RT的表达式_________(用题中给的字母Im、r、E、R表示);
(3)利用上面的表达式,根据不同温度下的R,可以算出对应RT的数值,部分计算结果已经标在坐标纸上,请补齐其余的数据,并作出RT-t曲线_________;
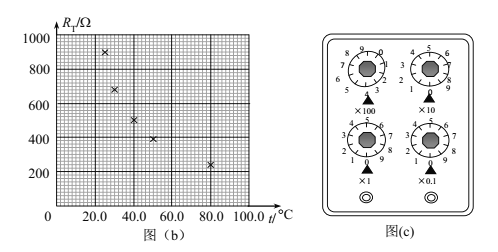
(4)将RT握于手心,调节R,使电流表读数半偏,此时R的读数如图(c)所示,该读数为____,手心温度为_________![]() 。
。