题目内容
18.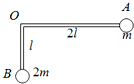 质量不计的直角形支架两端分别连接质量为m和2m的小球A和B.支架的两直角边长度分别为2l和l,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示.开始时OA边处于水平位置,由静止释放,则( )
质量不计的直角形支架两端分别连接质量为m和2m的小球A和B.支架的两直角边长度分别为2l和l,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示.开始时OA边处于水平位置,由静止释放,则( )| A. | A、B两球的最大速度之比v1:v2=1:1 | |
| B. | A球与B球组成的系统机械能守恒 | |
| C. | A球的速度最大时,两小球的总重力势能最小 | |
| D. | A球的速度最大时,两直角边与竖直方向的夹角为45° |
分析 AB两个球组成的系统机械能守恒,但对于单个的球来说机械能是不守恒的,根据系统的机械能守恒列式可以求得AB之间的关系,同时由于AB是同时转动的,它们的角速度的大小相同.
解答 解:A、根据题意知两球的角速度相同,线速度之比为VA:VB=ω•2l:ω•l=2:1,故A错误;
BC、系统只有重力做功,故机械能守恒,可知两球总重力势能最小时,二者的动能最大,故BC正确;
D、当OA与竖直方向的夹角为θ时,由机械能守恒得:
mg•2lcosθ-2mg•l(1-sinθ)=$\frac{1}{2}$mVA2+$\frac{1}{2}$•2mVB2,
解得:VA2=$\frac{8}{3}$gl(sinθ+cosθ)-$\frac{8}{3}$gl,
由数学知识知,当θ=45°时,sinθ+cosθ有最大值,故D正确;
故选:BCD
点评 本题中的AB的位置关系并不是在一条直线上,所以在球AB的势能的变化时要注意它们之间的关系,在解题的过程中还要用到数学的三角函数的知识,要求学生的数学基本功要好,本题由一定的难度.

练习册系列答案
相关题目
9.a、b两个电容器如图1所示,图2是它们的部分参数.由此可知,a、b两个电容器的电容之比为( )


| A. | 1:10 | B. | 4:5 | C. | 8:1 | D. | 64:1 |
6.两颗行星绕太阳运动轨道的半长轴分别为a1和a2,且a1=4a2,则它们的周期之比T1:T2是( )
| A. | 16:1 | B. | 8:1 | C. | 4:1 | D. | 2:1 |
13. 在如图所示的电路中,电源的负极接地,其电动势为E、内电阻为r,R1、R2为定值电阻,R3为滑动变阻器,C为电容器,A、V为理想电流表和电压表.在滑动变阻器滑动头P自a端向b端滑动的过程中,下列说法中正确的是( )
在如图所示的电路中,电源的负极接地,其电动势为E、内电阻为r,R1、R2为定值电阻,R3为滑动变阻器,C为电容器,A、V为理想电流表和电压表.在滑动变阻器滑动头P自a端向b端滑动的过程中,下列说法中正确的是( )
 在如图所示的电路中,电源的负极接地,其电动势为E、内电阻为r,R1、R2为定值电阻,R3为滑动变阻器,C为电容器,A、V为理想电流表和电压表.在滑动变阻器滑动头P自a端向b端滑动的过程中,下列说法中正确的是( )
在如图所示的电路中,电源的负极接地,其电动势为E、内电阻为r,R1、R2为定值电阻,R3为滑动变阻器,C为电容器,A、V为理想电流表和电压表.在滑动变阻器滑动头P自a端向b端滑动的过程中,下列说法中正确的是( )| A. | 电压表示数变大 | B. | 电流表示数变大 | ||
| C. | 电容器C所带电荷量增多 | D. | a点的电势降低 |
3.真空中两个完全相同的金属小球,分别带有+4q和-2q的电荷.相距 r时库仑力为F.若将两小球接触以下又放回原位置,此时它们之间的库仑力为( )
| A. | F | B. | 2F | C. | $\frac{1}{2}$F | D. | $\frac{1}{8}$F |
7.关于时刻和时间间隔,下列说法正确的是( )
| A. | 作息时间表上的数字均表示时间间隔 | |
| B. | 时刻表示时间极短,时间间隔表示时间较长 | |
| C. | 手表上指针指示的是时间间隔 | |
| D. | “宁停三分,不抢一秒”指的是时间间隔 |
 测定木块与长木板之间的动摩擦因数时,采用如图所示的装置,图中长木板水平固定.
测定木块与长木板之间的动摩擦因数时,采用如图所示的装置,图中长木板水平固定.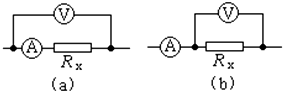 在伏安法测电阻的实验中,待测电阻Rx的阻值约为200Ω,电压表V的内阻约为2kΩ,电流表A的内阻约为10Ω,测量电路中电流表的连接方式如图(a)或图(b)所示,结果由公式Rx=$\frac{U}{I}$计算得出,式中U与I分别为电压表和电流表的示数.若将图(a)和图(b)中电路测得的电阻值分别记为Rx1和Rx2,则Rx1(选填“Rx1”或“Rx2”)更接近待测电阻的真实值,且测量值Rx1大于(选填“大于”“等于”或“小于”)真实值,测量值Rx2小于(选填“大于”“等于”或“小于”)真实值.若电压表V的内阻为2kΩ,电流表A的内阻约为10Ω,测电阻Rx的阻值应采用外接法(选填“内接法”“外接法”或“内外接均可以”)求得真实值(忽略读数误差).
在伏安法测电阻的实验中,待测电阻Rx的阻值约为200Ω,电压表V的内阻约为2kΩ,电流表A的内阻约为10Ω,测量电路中电流表的连接方式如图(a)或图(b)所示,结果由公式Rx=$\frac{U}{I}$计算得出,式中U与I分别为电压表和电流表的示数.若将图(a)和图(b)中电路测得的电阻值分别记为Rx1和Rx2,则Rx1(选填“Rx1”或“Rx2”)更接近待测电阻的真实值,且测量值Rx1大于(选填“大于”“等于”或“小于”)真实值,测量值Rx2小于(选填“大于”“等于”或“小于”)真实值.若电压表V的内阻为2kΩ,电流表A的内阻约为10Ω,测电阻Rx的阻值应采用外接法(选填“内接法”“外接法”或“内外接均可以”)求得真实值(忽略读数误差).