题目内容
9. 一质量为m、两端有挡板的小车静止在光滑水平面上,两挡板间距离为1.1m,在小车正中放一质量为m、长度为0.1m的物块,物块与小车间动摩擦因数μ=0.15.如图示,现给物块一个水平向右的瞬时冲量,使物块获得v0=6m/s的水平初速度.物块与挡板碰撞时间极短且无能量损失.求:
一质量为m、两端有挡板的小车静止在光滑水平面上,两挡板间距离为1.1m,在小车正中放一质量为m、长度为0.1m的物块,物块与小车间动摩擦因数μ=0.15.如图示,现给物块一个水平向右的瞬时冲量,使物块获得v0=6m/s的水平初速度.物块与挡板碰撞时间极短且无能量损失.求:(1)小车获得的最终速度;
(2)物块相对小车滑行的路程;
(3)物块与两挡板最多碰撞了多少次;
(4)物块最终停在小车上的位置.
分析 (1)当物块相对小车静止时,它们以共同的速度v做匀速直线运动,物块和小车相互作用过程中,系统动量守恒,根据动量守恒定律求解;
(2)对物块运动的全过程,根据动能定理求出物块相对小车滑行的路程;
(3)先求出物块第一次与小车相撞时,相对于小车运动的路程,再求出此后每次相撞物块相对于小车运动的路程,进而根据总路程求解相撞的次数;
(4)根据相撞的次数和总路程的关系判断物块最终停在小车上的位置.
解答 解:(1)当物块相对小车静止时,它们以共同的速度v做匀速直线运动,物块和小车相互作用过程中,系统动量守恒,
以v0的方向为正方向,根据动量守恒定律得:
mv0=(m+m)v
解得:v=3m/s
(2)对物块运动的全过程,根据动能定理得:
$\frac{1}{2}m{v}^{2}-\frac{1}{2}m{{v}_{0}}^{2}=-μmgs$
解得:s=6m
(3)物块第一次与小车相撞时,相对于小车运动的路程为$l=\frac{1.1-0.1}{2}=0.5m$,此后物块每相对于小车运动1m路程与小车碰撞一次,
则相撞的次数n=$\frac{s-0.5}{l-d}+1=\frac{6-0.5}{1.1-0.1}+1=6.5$
所以物块与两挡板最多碰撞了6次
(4)根据第三问可知,相撞6次后,物块又相对小车运动了0.5m,所以小车最终还停在小车正中处.
答:(1)小车获得的最终速度为3m/s;
(2)物块相对小车滑行的路程为6m;
(3)物块与两挡板最多碰撞了6次;
(4)物块最终停在小车上的正中处.
点评 本题主要考查了动量守恒定律以及动能定理的直接应用,注意应用动量守恒定律时要规定正方向,特别注意本题中物块不能看成质点.

练习册系列答案
相关题目
19.一个物体,在5s的时间内通过了20m的位移,则它的平均速度是( )
| A. | 4m∕s | B. | 5m∕s | C. | 6m∕s | D. | 10m∕s |
7. 如图所示,高度为L、横截面积为s的物块浮在盛水的杯内,杯内水的高度恰好为L.已知杯子的横截面积为2s,水的密度为ρ0,物块的密度为$\frac{{ρ}_{0}}{2}$,现用外力将物块按入水底,则外力所做的功至少是( )
如图所示,高度为L、横截面积为s的物块浮在盛水的杯内,杯内水的高度恰好为L.已知杯子的横截面积为2s,水的密度为ρ0,物块的密度为$\frac{{ρ}_{0}}{2}$,现用外力将物块按入水底,则外力所做的功至少是( )
 如图所示,高度为L、横截面积为s的物块浮在盛水的杯内,杯内水的高度恰好为L.已知杯子的横截面积为2s,水的密度为ρ0,物块的密度为$\frac{{ρ}_{0}}{2}$,现用外力将物块按入水底,则外力所做的功至少是( )
如图所示,高度为L、横截面积为s的物块浮在盛水的杯内,杯内水的高度恰好为L.已知杯子的横截面积为2s,水的密度为ρ0,物块的密度为$\frac{{ρ}_{0}}{2}$,现用外力将物块按入水底,则外力所做的功至少是( )| A. | $\frac{1}{8}$ρ0gsL2 | B. | $\frac{1}{4}$ρ0gsL2 | C. | $\frac{5}{16}$ρ0gsL2 | D. | $\frac{3}{16}$ρ0gsL2 |
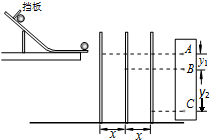 (1)在研究平抛运动的实验中,为了正确描绘出小球平抛运动的轨迹,在固定弧形斜槽时,应注意使斜槽末端切线水平;实验时,每次使小球由静止滚下都应注意从同一位置释放.
(1)在研究平抛运动的实验中,为了正确描绘出小球平抛运动的轨迹,在固定弧形斜槽时,应注意使斜槽末端切线水平;实验时,每次使小球由静止滚下都应注意从同一位置释放. 如图所示,在一个范围足够大、垂直纸面向里的匀强磁场中,用绝缘细线将金属棒吊起,使其呈水平状态.已知金属棒长L=0.25m,质量m=0.1kg,棒中通有I=10A的向右的电流,取g=10m/s2.求:
如图所示,在一个范围足够大、垂直纸面向里的匀强磁场中,用绝缘细线将金属棒吊起,使其呈水平状态.已知金属棒长L=0.25m,质量m=0.1kg,棒中通有I=10A的向右的电流,取g=10m/s2.求: 如图所示电路中,电阻R1=6Ω,R2=3Ω,R3=2Ω,R4=12Ω,求外电路的总电阻.
如图所示电路中,电阻R1=6Ω,R2=3Ω,R3=2Ω,R4=12Ω,求外电路的总电阻.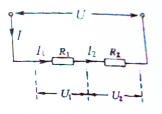 电阻R1、R2串联在电路中,总电压为U,总电流为I,则:
电阻R1、R2串联在电路中,总电压为U,总电流为I,则: 如图所示,墙角吊着一盏电灯,若水平绳的拉力为3N,BO绳的粒力为5N,求:
如图所示,墙角吊着一盏电灯,若水平绳的拉力为3N,BO绳的粒力为5N,求: