题目内容
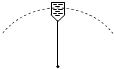
如图所示，一细杆与水桶相连，水桶中装有水，水桶与细杆一起在竖直平面内做圆周运动，水桶中水的质量 m=0.5kg，水的重心到转轴 O 的距离 L=50cm，g 取 10m/s2．（1）若水桶转至最高点时水不流出来，求水桶的最小速率．（结果可用根式表示）
（2）若在最高点时水桶的速率 v=3m/s，求水对桶底的压力大小．
【答案】分析：（1）水桶运动到最高点时，水不流出恰好不流出时由水受到的重力刚好提供其做圆周运动的向心力，根据牛顿第二定律求解最小速率；
（2）水在最高点速率v=3m/s时，以水为研究对象，分析受力情况：重力和桶底的弹力，其合力提供水做圆周运动的向心力，由牛顿第二定律求解此弹力，再牛顿第三定律，水对桶的压力大小．
解答：解：（1）水桶运动到最高点时，设速度为v时恰好水不流出，由水受到的重力刚好提供其做圆周运动的向心力，根据牛顿第二定律得：mg=m
解得：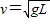
=
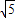m/s
（2）设桶运动到最高点对水的弹力为F，则水受到重力和弹力提供向心力，根据牛顿第二定律，有：
mg+F=m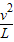
解得：F=m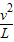
-mg=4N
根据牛顿第三定律，水对桶的压力大小：F'=F=4N
答：（1）若水桶转至最高点时水不流出来，水桶的最小速率为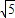
m/s；
（2）若在最高点时水桶的速率 v=3m/s，水对桶底的压力大小为4N．
点评：本题应用牛顿第二定律破解水流星节目成功的奥秘，关键在于分析受力情况，确定向心力的来源．
（2）水在最高点速率v=3m/s时，以水为研究对象，分析受力情况：重力和桶底的弹力，其合力提供水做圆周运动的向心力，由牛顿第二定律求解此弹力，再牛顿第三定律，水对桶的压力大小．
解答：解：（1）水桶运动到最高点时，设速度为v时恰好水不流出，由水受到的重力刚好提供其做圆周运动的向心力，根据牛顿第二定律得：mg=m
解得：
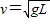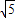=m/s（2）设桶运动到最高点对水的弹力为F，则水受到重力和弹力提供向心力，根据牛顿第二定律，有：
mg+F=m
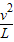
解得：F=m
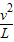-mg=4N根据牛顿第三定律，水对桶的压力大小：F'=F=4N
答：（1）若水桶转至最高点时水不流出来，水桶的最小速率为
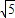m/s；（2）若在最高点时水桶的速率 v=3m/s，水对桶底的压力大小为4N．
点评：本题应用牛顿第二定律破解水流星节目成功的奥秘，关键在于分析受力情况，确定向心力的来源．
练习册系列答案
智能训练练测考系列答案
相关题目
如图所示，一细杆与水桶相连，水桶中装有水，水桶与细杆一起在竖直平面内做圆周运动，水桶中水的质量 m=0.5kg，水的重心到转轴 O 的距离 L=50cm，g 取 10m/s2．
（2012?上海模拟）如图所示，一根长为L=2m的细刚性轻杆的两端分别连结小球a和b，它们的质量分别为ma=8kg和mb=1kg，杆可绕距a球为
