题目内容
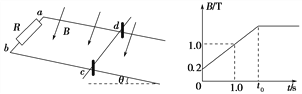
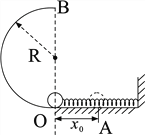
【题目】如图所示，轻弹簧的一端固定在墙上，另一端与置于粗糙水平面上质量为m的小球接触但不连接。开始时小球位于O点，弹簧水平且无形变。O点的左侧有一竖直放置的光滑半圆弧轨道，圆弧的半径为R ，B为轨道最高点，小球与水平面间的动摩擦因数为μ。现用外力推动小球，将弹簧压缩至A点，OA间距离为x0，将球由静止释放，小球恰能沿轨道运动到最高点B。已知弹簧始终在弹性限度内，重力加速度为g。下列说法中正确的是
A. 小球在从A到O运动的过程中速度不断增大
B. 小球运动过程中的最大速度为
C. 小球与弹簧作用的过程中，弹簧的最大弹性势能Ep=
D. 小球通过圆弧轨道最低点时，对轨道的压力为 5mg
【答案】C
【解析】小球在从A到O运动的过程中，受弹力和摩擦力，由牛顿第二定律可知： 
，物体做加速度减小的加速运动，当加速度为零的时（弹力等于摩擦力时）速度最大，接下来摩擦力大于弹力，小球开始做减速运动，当弹簧原长时离开弹簧，故A错误；因为小球恰能沿轨道运动到最高点B，由重力提供向心力： 
，解得： 
，从O到B根据动能定理得： 
，联立以上解得： 
， 由上分析可知：小球从开始运动到离开弹簧速度先增大后减小，所以最大速度要比
大，故B错误；从A到O根据能量守恒得： 
，联立以上得： 
，故C正确；小球在最低点时做圆周运动，由牛顿第二定律得： 
，联立以上解得： 
，故D错误。所以C正确，ABD错误。
练习册系列答案
相关题目
