题目内容
6.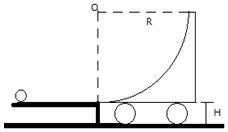 如图所示,由光滑的四分之一圆弧构成的小车质量为 M,质量为 m 的小球以速度v0冲上静止在光滑水平面的小车.已知 M=1kg,m=2kg,R=0.6m,H=0.45m,重力加速度 g 取 10m/s2.
如图所示,由光滑的四分之一圆弧构成的小车质量为 M,质量为 m 的小球以速度v0冲上静止在光滑水平面的小车.已知 M=1kg,m=2kg,R=0.6m,H=0.45m,重力加速度 g 取 10m/s2.(1)若小球刚好能到达小车的最高点,求v0的值.
(2)若v0 满足(1)的条件,求小车能获得的最大速度.
(3)若v0=9m/s,求小球落地时与小车最左端的距离.
分析 (1)依题意可知,当小球刚好到达小车最高点时,小球和小车只具有共同的水平速度,由水平动量守恒和能量守恒定律列式求解;
(2)当小球返回到小车最左端时,小车获得的速度最大,由水平动量守恒和能量守恒定律列式求解;
(3)当v0=9m/s时,小球冲出小车做斜抛运动后,从新落到小车上,小球返回小车最左端,由水平动量守恒和能量守恒定律求出速度,小球从小车最左端离开小车,向前做平抛运动,由平抛运动公式列式求解.
解答 解:(1)依题意可知,当小球刚好到达小车最高点时,小球和小车只具有共同的水平速度,由水平动量守恒和能量守恒定律得:
mv0=(M+m)v共,
$\frac{1}{2}m{{v}_{0}}^{2}=\frac{1}{2}(m+M){{v}_{共}}^{2}+mgR$,
解得:v0=6m/s
(2)当小球返回到小车最左端时,小车获得的速度最大,由水平动量守恒和能量守恒定律得:
mv0=Mv1+mv2,$\frac{1}{2}m{{v}_{0}}^{2}=\frac{1}{2}M{{v}_{1}}^{2}+\frac{1}{2}m{{v}_{2}}^{2}$,
解得:v1=8m/s,v2=2m/s,
(3)当v0=9m/s时,小球冲出小车做斜抛运动后,从新落到小车上,小球返回小车最左端,由水平动量守恒和能量守恒定律得:
mv0=Mv3+mv4,
$\frac{1}{2}m{{v}_{0}}^{2}=\frac{1}{2}M{{v}_{3}}^{2}+\frac{1}{2}m{{v}_{4}}^{2}$,
解得:v3=12m/s,v4=3m/s,
小球从小车最左端离开小车,向前做平抛运动,由平抛运动公式得:
$H=\frac{1}{2}g{t}^{2}$,
△x=(v3-v4)t=2.7m.
答:(1)若小球刚好能到达小车的最高点,v0的值为6m/s.
(2)若v0 满足(1)的条件,则小车能获得的最大速度为8m/s.
(3)若v0=9m/s,小球落地时与小车最左端的距离为2.7m.
点评 本题主要考查了动量守恒定律以及能量守恒定律的直接应用,解题时要注意当小球刚好到达小车最高点时,小球和小车只具有共同的水平速度,竖直方向动量不守恒,难度适中.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 5$\sqrt{3}$N | B. | 5N | C. | 10N | D. | 仍为零 |

| A. | A图中无光电子射出 | |
| B. | B图中光电子到达金属板时的动能大小为1.5eV | |
| C. | C图中的光电子能到达金属网 | |
| D. | D图中光电子到达金属板时的最大动能为3.5eV |
| A. | 在测量电阻时,更换倍率后必须重新进行调零 | |
| B. | 在测量电流时,更换量程后必须重新进行调零 | |
| C. | 在测量未知电阻时,必须先选择倍率最大挡进行试测 | |
| D. | 在测量未知电流时,必须先选择电流最大量程进行试测 |
| A. | “墨子”号卫星的运行速度比天宫二号大 | |
| B. | “墨子”号卫星的运行周期比天宫二号小 | |
| C. | “墨子”号卫星的向心加速度比天宫二号小 | |
| D. | “墨子”号卫星和天宫二号的运行速度都可能大于7.9 km/s |
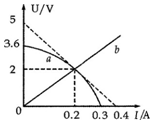 硅光电池是一种太阳能电池,具有低碳环保的优点.如图所示,图线a是该电池在某光照强度下路端电压U和电流I的关系图象(电池内阻不是常数),图线b是某电阻R的U-I图象.在该光照强度下将它们组成闭合回路时,下列相关叙述说法正确的是( )
硅光电池是一种太阳能电池,具有低碳环保的优点.如图所示,图线a是该电池在某光照强度下路端电压U和电流I的关系图象(电池内阻不是常数),图线b是某电阻R的U-I图象.在该光照强度下将它们组成闭合回路时,下列相关叙述说法正确的是( )| A. | 此时硅光电池的内阻为12.5Ω | B. | 此时硅光电池的输出功率为 0.2W | ||
| C. | 此时硅光电池的总功率为 0.72W | D. | 此时硅光电池的输出效率为 40% |
 如图所示,在光滑水平面上有ABC三个质量均为m的小球,A带正电,B带负电,C不带电,A,B带电量的绝对值均为Q,B,C两个小球用绝缘细绳连接在一起,当用外力F拉着A球向右运动时,B,C也跟着A球一起向右运动,在运动过程中三个小球保持相对静止共同运动,则( )
如图所示,在光滑水平面上有ABC三个质量均为m的小球,A带正电,B带负电,C不带电,A,B带电量的绝对值均为Q,B,C两个小球用绝缘细绳连接在一起,当用外力F拉着A球向右运动时,B,C也跟着A球一起向右运动,在运动过程中三个小球保持相对静止共同运动,则( )| A. | BC间绳的拉力大小为$\frac{2}{3}$F | B. | BC间绳的拉力大小为$\frac{1}{3}$F | ||
| C. | AB两球间距为$\sqrt{\frac{3K{Q}^{2}}{2F}}$ | D. | AB两球间距为$\sqrt{\frac{3K{Q}^{2}}{F}}$ |

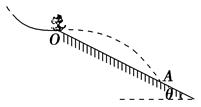 如图所示,一名跳台滑雪运动员经过一段时间的加速滑行后从O点水平飞出,经过3s落到斜坡上的A点.已知O点是斜坡的起点,斜坡与水平面的夹角θ=37°,运动员的质量m=50kg.不计空气阻力(sin 37°=0.6,cos 37°=0.8;g取10m/s2).求:
如图所示,一名跳台滑雪运动员经过一段时间的加速滑行后从O点水平飞出,经过3s落到斜坡上的A点.已知O点是斜坡的起点,斜坡与水平面的夹角θ=37°,运动员的质量m=50kg.不计空气阻力(sin 37°=0.6,cos 37°=0.8;g取10m/s2).求: