题目内容
15.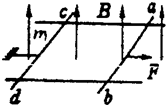 如图所示,在方向竖直向上的磁感应强度为B的匀强磁场中,有两条光滑的平行金属导轨,其电阻不计,间距为L,导轨平面与磁场方向垂直,ab、cd为两根垂直导轨放置的、电阻都为R、质量都为m的金属棒,棒cd用最大拉力为f的水平细线拉住,棒ab在水平拉力F的作用下以加速度a向右做匀加速运动.求:
如图所示,在方向竖直向上的磁感应强度为B的匀强磁场中,有两条光滑的平行金属导轨,其电阻不计,间距为L,导轨平面与磁场方向垂直,ab、cd为两根垂直导轨放置的、电阻都为R、质量都为m的金属棒,棒cd用最大拉力为f的水平细线拉住,棒ab在水平拉力F的作用下以加速度a向右做匀加速运动.求:(1)F随时间的变化规律.
(2)经多长时间细线将被拉断?
(3)若在细线被拉断的瞬间撤去拉力F,则棒ab和棒cd的最终速度为多大?
(4)从细线断开到两金属棒达到最终速度,电路中产生了多少热量?
分析 (1)根据速度时间公式求出速度的表达式,从而根据切割产生的感应电动势和闭合电路欧姆定律求出电流的大小,得出安培力的大小,根据牛顿第二定律求出水平拉力F随时间的变化规律.
(2)对CD棒分析,当CD棒所受的安培力等于绳子的最大拉力时,绳子断裂,抓住共点力平衡求出细线将被拉断的时间.
(3)若在细线被拉断的瞬间撤去拉力F,则棒ab和棒cd的组成的系统在水平方向不受力,满足动量守恒定律,由动量守恒定律列式即可求出最终速度;
(4)从细线断开到两金属棒达到最终速度的过程中,由于产生感应电动势和感应电流,杆的动能转化为内能,由功能关系即可求出电路中产生的热量.
解答 解:(1)在时刻t,棒的速度:v=a t
棒中感应电动势为:E=B L v=B L a t
棒中的感应电流为:I=$\frac{BLat}{2R}$
由牛顿第二定律有:F-BIL=ma
得:F=$\frac{{{B^2}{L^2}a}}{2R}t+ma$
(2)细线拉断时满足:
BIL=T0
即:$\frac{{B}^{2}{L}^{2}a}{2R}t=f$
解得:t=$\frac{2Rf}{{B}^{2}{L}^{2}a}$
(3)撤去拉力时,杆ab的速度:v=at=$a×\frac{2Rf}{{B}^{2}{L}^{2}a}=\frac{2Rf}{{B}^{2}{L}^{2}}$
撤去拉力F后则棒ab和棒cd的组成的系统在水平方向不受力,满足动量守恒定律,选择向右为正方向,设最终的速度为v′,得:
mv=(m+m)v′
联立得:$v′=\frac{Rf}{{B}^{2}{L}^{2}}$
(4)撤去拉力后系统减少的动能转化为内能,则:
$Q=\frac{1}{2}m{v}^{2}-\frac{1}{2}×2mv{′}^{2}$
联立得:Q=$\frac{m{f}^{2}{R}^{2}}{{B}^{4}{L}^{4}}$
答:(1)线断以前水平拉力F随时间t的变化规律为F=$\frac{{{B^2}{L^2}a}}{2R}t+ma$;
(2)经过时间$\frac{2Rf}{{B}^{2}{L}^{2}a}$细线将被拉断..
(3)若在细线被拉断的瞬间撤去拉力F,则棒ab和棒cd的最终速度为$\frac{Rf}{{B}^{2}{L}^{2}}$;
(4)从细线断开到两金属棒达到最终速度,电路中产生了热量是$\frac{m{f}^{2}{R}^{2}}{{B}^{4}{L}^{4}}$.
点评 本题考查了电磁感应与力学的综合,虽然题目的情景设置比较常见,但是4个小问 涉及到的知识点比较多,在解答的过程中要理清思路,把握相应的规律与公式.

| A. | 电流表示数增大 | B. | 电压表示数减小 | ||
| C. | 两表示数同时增大 | D. | 两表示数同时减小 |

| A. | 甲是波动图象,乙是振动图象,波速是2m/s | |
| B. | 甲是波动图象,乙是振动图象,波速是1m/s | |
| C. | 甲是振动图象,乙是波动图象,波速是2m/s | |
| D. | 甲是振动图象,乙是波动图象,波速是1m/s |
| A. | 1:2:3 | B. | 1:3:5 | C. | 1:4:9 | D. | 1:8:27 |

 在用油膜法估测油酸分子的大小的实验中,用到器材有:浓度为0.05%(体积分数)的油酸酒精溶液、最小刻度为0.1mL的量筒、盛有适量清水的45×50cm2浅盘、痱子粉、橡皮头滴管、玻璃板、彩笔、坐标纸.实验步骤如下:
在用油膜法估测油酸分子的大小的实验中,用到器材有:浓度为0.05%(体积分数)的油酸酒精溶液、最小刻度为0.1mL的量筒、盛有适量清水的45×50cm2浅盘、痱子粉、橡皮头滴管、玻璃板、彩笔、坐标纸.实验步骤如下: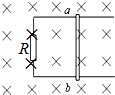 如图所示,水平放置的平行金属导轨相距l=0.50m,左端接一电阻R=0.20欧,磁感应强度B=0.40T的匀强磁场,方向垂直于导轨平面,导体棒ab垂直放在导轨上,并能无摩擦的沿导轨滑动,导轨和导体棒的电阻均可忽略不计,当ab以=4.0m/s的速度水平向右匀速滑动时,求:
如图所示,水平放置的平行金属导轨相距l=0.50m,左端接一电阻R=0.20欧,磁感应强度B=0.40T的匀强磁场,方向垂直于导轨平面,导体棒ab垂直放在导轨上,并能无摩擦的沿导轨滑动,导轨和导体棒的电阻均可忽略不计,当ab以=4.0m/s的速度水平向右匀速滑动时,求:
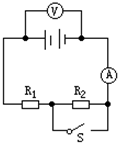
 如图所示,电源电动势E=40V,R=24Ω,M为一线圈电阻r M=0.4Ω的电动机.当开关S断开时,理想电流表的示数为I1=1.6A;当开关S闭合时,电流表的示数为I2=4.0A.求
如图所示,电源电动势E=40V,R=24Ω,M为一线圈电阻r M=0.4Ω的电动机.当开关S断开时,理想电流表的示数为I1=1.6A;当开关S闭合时,电流表的示数为I2=4.0A.求