Question

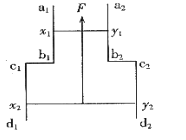
【题目】如图所示，楔形木块abc固定在水平面上，粗糙斜面ab和粗糙斜面bc与水平面的夹角相同，顶角b处安装一个定滑轮。质量分别为M、m(Mm)的滑块，通过不可伸长的轻绳跨过定滑轮连接，轻绳与斜面平行。两滑块由静止释放后，沿斜面做匀加速运动。若不计滑轮的质量和摩擦，在两滑块沿斜面运动的过程中（ ）

A. 轻绳对m做的功等于m机械能的增加

B. 重力对M做的功小于M减少的重力势能

C. 轻绳对m做的功等于m增加的动能与m克服摩擦力所做的功之和

D. 两滑块与轻绳组成的系统的机械能损失等于M、m克服摩擦力所做的功之和

Answer 1

【答案】D

【解析】

AC、根据动能定理可知，轻绳对m做的功等于m增加的机械能与m克服摩擦力所做的功之和，轻绳对m做的功大于m机械能的增加，故A、C错误。

B、根据重力做功与重力势能变化的关系可知，重力对M做的功等于M重力势能的变化，故B错误。

D、根据能量守恒定律，两滑块与轻绳组成的系统的机械能损失等于M、m克服摩擦力所做的功之和，故D正确。