Question

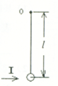
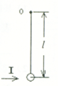宇航员在某一星球上以速度V₀竖直向上抛出一小球，经过时间t，小球又落到原抛出点，然后他用一根长为l的细绳把一个质量为m的小球悬挂在O点，使小球处于静止状态．如图所示，在最低点给小球一个水平向右的冲量I，使小球能在竖直平面内运动，若小球在运动的过程中始终对细绳有力的作用，则冲量I满足什么条件？

Answer 1

分析：由竖直上抛运动公式求得该星球的重力加速度，当小球摆到与悬点等高处时，细绳刚好松弛，小球对细绳无力作用，则小球在最低点有最大速度，若经过最高点细绳刚好松弛，小球对细绳无力作用，则小球在最低点的最小速度，根据机械能守恒定律和动量定理即可求解范围．

解答：解：设星球表面附近的重力加速度为g，由竖直上抛运动公式：t=

2v0

g

得g=

2v0

t

当小球摆到与悬点等高处时，细绳刚好松弛，小球对细绳无力作用，则小球在最低点有最大速度，由机械能守恒定律得：mgl=

1

2

mv12．由动量定理得：I1=mv1=m

v0l t

当小球做完整的圆周运动时，设最高点的最小速度为v′，由mg=m

v′2

l

，解得v′=

gl

，
若经过最高点细绳刚好松弛，小球对细绳无力作用，则小球在最低点的最小速度为v₂．
则由机械能守恒定律得：

1

2

mv22=2mgl+

1

2

mv′2，
动量定理有：
I₂=mv₂
解得：I₂=m

10v0l t

．
所以冲量I满足I＞m

10v0l t

或I＜m

v0l t

答：若小球在运动的过程中始终对细绳有力的作用，则冲量I满足I＞m

10v0l t

或I＜m

v0l t

点评：本题主要考查了机械能守恒定律、动量定理及向心力公式的直接应用，注意小球不能过与圆心等高的点的情况也符合要求，难度适中．