题目内容
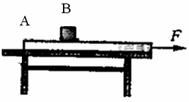
 如图所示,薄木板A长l=5.0m,质量M=5.0Kg,放在水平桌面上,板右端与桌面相齐,在A上距右端s=3.0m处放一小物块B,质量m=2.0Kg.已知A、B间动摩擦因数μ1=0.1,A与桌面间和B与桌面间的动摩擦因数均为μ2=0.2,原来系统静止.现对平板A施加一个水平向右、大小恒定的拉力F,作用一段时间,将平板A从小物块B的下面抽出,且小物块B最后恰好停在桌面的右端边缘.(取g=10m/s2),求:
如图所示,薄木板A长l=5.0m,质量M=5.0Kg,放在水平桌面上,板右端与桌面相齐,在A上距右端s=3.0m处放一小物块B,质量m=2.0Kg.已知A、B间动摩擦因数μ1=0.1,A与桌面间和B与桌面间的动摩擦因数均为μ2=0.2,原来系统静止.现对平板A施加一个水平向右、大小恒定的拉力F,作用一段时间,将平板A从小物块B的下面抽出,且小物块B最后恰好停在桌面的右端边缘.(取g=10m/s2),求:(1)B从初位置运动到桌边的时间t;
(2)拉力F的大小.
分析:AB未分离时采用隔离法对AB进行受力分析根据牛顿第二定律列方程求出其加速度,由位移速度公式表示出二者的位移,B从A上掉下时利用其位移之差为3m列方程求出B掉下时的速度,然后根据速度时间公式求出B在A上运动时间与B匀减速运动到桌边经历的时间;
先由位移速度公式求出自A开始运动至B从A上掉下的这一过程中,B的位移为s1B、A的位移为s1A,利用其位移关系求出A的加速度,然后根据牛顿第二定律对A列方程求出拉力的大小.
先由位移速度公式求出自A开始运动至B从A上掉下的这一过程中,B的位移为s1B、A的位移为s1A,利用其位移关系求出A的加速度,然后根据牛顿第二定律对A列方程求出拉力的大小.
解答:解:(1)对于B,在未离开A时,其运动加速度大小为:a1=
=μ1g=1m/s2①
B从A上掉下来后,B在桌面的摩擦力作用下做减速运动,其加速度大小为:a2=
=μ2g=2m/s2②
设B从A上掉下时,其速度为v,则由题给条件应有:
-
=s③
由①②③联立且代入数据解得:v=2m/s
设自A开始运动至B从A上掉下的这一过程中,经历的时间为t1、B减速运动到桌边经历时间为t2,则:
t1=
=2s ④
t2=
=1s⑤
故B运动的时间是:t=t1+t2=3s ⑥
(2)设自A开始运动至B从A上掉下的这一过程中,B的位移为s1B、A的位移为s1A,则:
slB=
=2m ⑦
slA=(l-s)+slB=2m+2m=4m ⑧
以aA表示这段时间内A的加速度,则有slA=
aAt12 ⑨
对A由牛顿第二定律应有F-μ1mg-μ2(M+m)g=MaA ⑩
代入数据解得:F=26N
答:(1)B从初位置运动到桌边的时间t为3s;
(2)拉力F的大小为26N.
| μ1mg |
| m |
B从A上掉下来后,B在桌面的摩擦力作用下做减速运动,其加速度大小为:a2=
| μ2mg |
| m |
设B从A上掉下时,其速度为v,则由题给条件应有:
| v2 |
| 2a1 |
| v2 |
| 2a2 |
由①②③联立且代入数据解得:v=2m/s
设自A开始运动至B从A上掉下的这一过程中,经历的时间为t1、B减速运动到桌边经历时间为t2,则:
t1=
| v |
| a1 |
t2=
| v |
| a2 |
故B运动的时间是:t=t1+t2=3s ⑥
(2)设自A开始运动至B从A上掉下的这一过程中,B的位移为s1B、A的位移为s1A,则:
slB=
| v2 |
| 2a1 |
slA=(l-s)+slB=2m+2m=4m ⑧
以aA表示这段时间内A的加速度,则有slA=
| 1 |
| 2 |
对A由牛顿第二定律应有F-μ1mg-μ2(M+m)g=MaA ⑩
代入数据解得:F=26N
答:(1)B从初位置运动到桌边的时间t为3s;
(2)拉力F的大小为26N.
点评:本题主要考查了牛顿第二定律及运动学基本公式的直接应用,抓住位移之间的关系解题,难度适中.

练习册系列答案
相关题目
 如图所示,轻质弹簧的一端固定在地面上,另一端与质量为M=1.5Kg的薄木板A相连,质量为m=0.5Kg的小球B放在木板A上,弹簧的劲度系数为k=2000N/m.现有一竖直向下、大小F=20N的力作用在B上且系统处于静止状态,在B球正上方处由一四分之一内壁光滑竖直圆弧轨道,圆弧半径R=0.4m,圆弧下端P点距离距离弹簧原长位置高度为h=0.6m.撤去外力F后,B竖直上升最终从P点切入原轨道,到达Q点的速度为vQ=4m/s.(g=10m/s2).求:
如图所示,轻质弹簧的一端固定在地面上,另一端与质量为M=1.5Kg的薄木板A相连,质量为m=0.5Kg的小球B放在木板A上,弹簧的劲度系数为k=2000N/m.现有一竖直向下、大小F=20N的力作用在B上且系统处于静止状态,在B球正上方处由一四分之一内壁光滑竖直圆弧轨道,圆弧半径R=0.4m,圆弧下端P点距离距离弹簧原长位置高度为h=0.6m.撤去外力F后,B竖直上升最终从P点切入原轨道,到达Q点的速度为vQ=4m/s.(g=10m/s2).求:
 如图所示,薄木板A长l=5.0m,质量M=5.0kg,放在水平桌面上,板右端与桌面相齐,在A上距右端s=3.0m处放一小物块B,质量m=2.0kg,已知A、B间动摩擦因数μ1=0.1,A与桌面间和B与桌面间的动摩擦因数μ2=0.2,原来系统静止,现对平板A施加一个水平向右、大小恒定的拉力F,作用一段时间,将平板A从小物块B的下面抽出,且小物块B最后恰好停在桌面的右端边缘。取g=10m/s2,求:
如图所示,薄木板A长l=5.0m,质量M=5.0kg,放在水平桌面上,板右端与桌面相齐,在A上距右端s=3.0m处放一小物块B,质量m=2.0kg,已知A、B间动摩擦因数μ1=0.1,A与桌面间和B与桌面间的动摩擦因数μ2=0.2,原来系统静止,现对平板A施加一个水平向右、大小恒定的拉力F,作用一段时间,将平板A从小物块B的下面抽出,且小物块B最后恰好停在桌面的右端边缘。取g=10m/s2,求: