题目内容
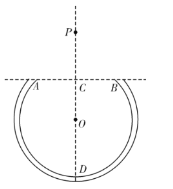
【题目】如图所示，一内壁光滑的绝缘圆管固定在竖直平面内，圆管围成的圆的圆心为O，D点为圆管的最低点，A、B两点在同一水平线上，AB=2L，该圆的半径为r=
L（圆管的内径忽略不计），过OD的虚线与过AB的虚线垂直相交于C点.在虚线AB的上方存在水平向左的、范围足够大的恒定风力场，物体在虚线的下方运动时会立即受到竖直向上的恒力，大小等于mg.圆心O正上方的P点有一质量为m 的小物体（视为质点），P、C间距为L.现将该小物体于P点无初速释放，经过一段时间，小物体刚好沿切线无碰撞地进入圆管内，并继续运动.重力加速度用g表示.
（1）小物体在虚线AB上方运动时受到的风力为多大？
（2）小物体从管口B离开后，经过一段时间的运动落到虚线AB上的N点（图中未标出N点），则N点距离C点多远？
（3）小物体由P点运动到N点的总时间为多少？
【答案】（1）mg.；（2）7L；（3）
【解析】
（1）小物体无初速释放后在重力G、风力F的作用下刚好沿切线无碰撞地进入圆管内，由几何关系知PA连线即A处圆管的切线，故小物体必沿PA连线做匀加速直线运动，重力与风力的合力沿PA方向；
又因为：
故：
，
解得：
F=mg
（2）小物体从P到A，由动能定理可得：
解得：
物体在虚线的下方运动时会受到竖直向上的恒力，大小等于mg，故小物体从A到B做匀速圆周运动，
小物体从管口 B离开后，经过一段时间的运动落到虚线AB上的N点，竖直方向：
，
解得：
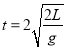
水平方向：
F=ma
解得：
x= 8L
N点距离C点：
xCN=x-L=7L
（3）设小物体从P到A的时间为t1，
则：
解得：
设物体从A到B的时间为t2，则
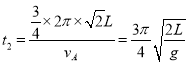
小物体由P点运动到N点的总时间：
.
练习册系列答案
相关题目
