题目内容
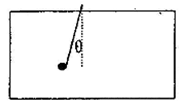
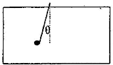 如图一个箱子放在水平地面上,质量为M,箱内用一长为L的细线拴一小球绳,另一端拴在箱子的顶板上,小球质量为m现把细绳拉到与竖直方向成θ角自由释放当球摆到最低点时,地面受到的压力为( )
如图一个箱子放在水平地面上,质量为M,箱内用一长为L的细线拴一小球绳,另一端拴在箱子的顶板上,小球质量为m现把细绳拉到与竖直方向成θ角自由释放当球摆到最低点时,地面受到的压力为( )分析:若球保持不动,压力为(M+m)g;小球摆动,根据动能定理求解最低点速度;在最低点,球受到的重力和拉力的合力提供向心力,与静止时相比,拉力增加值等于向心力大小;故压力的增加量也等于向心力的大小.
解答:解:若球保持不动,压力为(M+m)g;
小球摆动,根据动能定理,有:
mgl(1-cosθ)=
mv2
解得:v=
最低点,球受到的重力和拉力的合力提供向心力,与静止时相比,拉力增加值等于向心力大小,为:
Fn=m
=2mg(1-cosθ)
故此时压力为:N=(M+m)g+F=Mg+mg(3-2cosθ)
故选D.
小球摆动,根据动能定理,有:
mgl(1-cosθ)=
| 1 |
| 2 |
解得:v=
| 2gl(1-cosθ) |
最低点,球受到的重力和拉力的合力提供向心力,与静止时相比,拉力增加值等于向心力大小,为:
Fn=m
| v2 |
| l |
故此时压力为:N=(M+m)g+F=Mg+mg(3-2cosθ)
故选D.
点评:本题关键明确与静止时相比,压力增加了,增加量等于向心力的竖直分量.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 如图所示,一个箱子放在水平地面上,箱内有一固定的竖直杆,在杆上套着一个环,箱和杆的质量为M,环的质量为m,已知环沿着杆以加速度a加速下滑(a<g) 则此时箱对地面的压力N的大小是( )
如图所示,一个箱子放在水平地面上,箱内有一固定的竖直杆,在杆上套着一个环,箱和杆的质量为M,环的质量为m,已知环沿着杆以加速度a加速下滑(a<g) 则此时箱对地面的压力N的大小是( )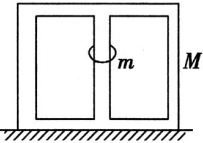 一个箱子放在水平地面上,箱内有一固定的竖直杆,在杆上套着一个环,箱子与杆的质量为M,环的质量为m,如图所示.已知环沿杆匀加速下滑时,环与杆间的摩擦力大小为Ff,则此时箱子对地面的压力大小为多少?
一个箱子放在水平地面上,箱内有一固定的竖直杆,在杆上套着一个环,箱子与杆的质量为M,环的质量为m,如图所示.已知环沿杆匀加速下滑时,环与杆间的摩擦力大小为Ff,则此时箱子对地面的压力大小为多少?