题目内容
14. 如图,有3块水平放置的长薄金属板a、b和c,a、b之间相距为L.紧贴b板下表面竖直放置半径为R的半圆形塑料细管,两管口正好位于小孔M、N处.板a与b、b与c之间接有电压可调的直流电源,板b与c间还存在方向垂直纸面向外的匀强磁场.当体积为V0、密度为ρ、电荷量为q的带负电油滴,等间隔地以速率v0从a板上的小孔竖直向下射入,调节板间电压Uba和Ubc,当Uba=U1、Ubc=U2时,油滴穿过b板M孔进入细管,恰能与细管无接触地从N孔射出.忽略小孔和细管对电场的影响,不计空气阻力,重力加速度为g.求:
如图,有3块水平放置的长薄金属板a、b和c,a、b之间相距为L.紧贴b板下表面竖直放置半径为R的半圆形塑料细管,两管口正好位于小孔M、N处.板a与b、b与c之间接有电压可调的直流电源,板b与c间还存在方向垂直纸面向外的匀强磁场.当体积为V0、密度为ρ、电荷量为q的带负电油滴,等间隔地以速率v0从a板上的小孔竖直向下射入,调节板间电压Uba和Ubc,当Uba=U1、Ubc=U2时,油滴穿过b板M孔进入细管,恰能与细管无接触地从N孔射出.忽略小孔和细管对电场的影响,不计空气阻力,重力加速度为g.求:(1)油滴进入M孔时的速度v1;
(2)b、c两板间的电场强度E和磁感应强度B的值;
(3)当油滴从细管的N孔射出瞬间,将Uba和B立即调整到Uba′和B′,使油滴恰好不碰到a板,且沿原路与细管无接触地返回穿过M孔,请给出Uba′和B′的结果.
分析 (1)油滴开始下落的过程中有重力、电场力做功,根据动能定理求出油滴进入M孔的速度.
(2)油滴进入电场、磁场共存区域,恰与细管无接触地从N孔射出,知电场力等于重力,洛伦兹力提供向心力,根据平衡求出电场强度的大小,根据洛伦兹力提供向心力求出磁感应强度的大小.
(3)若油滴恰不能撞到a板,且再返回并穿过M点速度为零,根据动能定理求出U′ba的大小,返回到N孔时速度大小不变,现向左偏转做匀速圆周运动,则磁感应强度的大小不变,方向改变.
解答 解:(1)油滴进入电场后,重力与电场力均做功,设到M点时的速度为v1,由动能定理:
$\frac{1}{2}$mv12-$\frac{1}{2}$mv02=mgL+qU1
考虑到m=ρV0
得:v1=$\sqrt{{v}_{0}^{2}+2gL+\frac{2q{U}_{1}}{ρ{v}_{0}}}$
(2)油滴进入电场、磁场共存区域,恰与细管无接触地从N孔射出,须电场力与重力平衡,有:
mg=qE
得:E=$\frac{ρ{V}_{0}g}{q}$
油滴在半圆形细管中运动时,洛伦兹力提供向心力,有:qv1B=$m\frac{{v}_{1}^{2}}{R}$
得:B=$\frac{m{v}_{1}}{qR}$=$\frac{ρ{V}_{0}}{qR}$$\sqrt{{v}_{0}^{2}+2gL+\frac{2q{U}_{1}}{ρ{v}_{0}}}$
(3)若油滴恰不能撞到a板,且再返回并穿过M点,由动能定理,有:
0-$\frac{1}{2}$mv12=-mgL-qUba′
得:Uba′=U1+$\frac{ρ{v}_{0}}{qR}$$\sqrt{{v}_{0}^{2}+2gL+\frac{2q{U}_{1}}{ρ{v}_{0}}}$
考虑到油滴返回时速度方向已经相反,为了使油滴沿原路与细管无接触地返回并穿过M孔,磁感应强度的大小不变,方向相反,即:
B′=-B
答:(1)油滴进入M孔时的速度为$\sqrt{{v}_{0}^{2}+2gL+\frac{2q{U}_{1}}{ρ{v}_{0}}}$.
(2)b、c两板间的电场强度为$\frac{ρ{V}_{0}g}{q}$,磁感应强度为$\frac{ρ{V}_{0}}{qR}$$\sqrt{{v}_{0}^{2}+2gL+\frac{2q{U}_{1}}{ρ{v}_{0}}}$.
(3)U1′和B′分别为:U1+$\frac{ρ{v}_{0}}{qR}$$\sqrt{{v}_{0}^{2}+2gL+\frac{2q{U}_{1}}{ρ{v}_{0}}}$、-B.
点评 本题考查带电粒子在复合场中的运动,关键理清粒子的运动情况,结合牛顿第二定律和动能定理进行求解.

| A. | 物体运动时,速度的变化量越大,它的加速度一定越大 | |
| B. | 速度很大的物体,其加速度不可能为零 | |
| C. | 某时刻物体的速度为零,其加速度不可能很大 | |
| D. | 加速度方向一定与速度变化量的方向相同 |
 2014年8月25日,在我国南京举行的青奥会上,18岁的江苏选手吴圣平高难度的动作夺得三米板女子跳水冠军.起跳前,吴圣平在跳板的最外端静止站立时,如图所示,则( )
2014年8月25日,在我国南京举行的青奥会上,18岁的江苏选手吴圣平高难度的动作夺得三米板女子跳水冠军.起跳前,吴圣平在跳板的最外端静止站立时,如图所示,则( )| A. | 吴圣平对跳板的压力方向竖直向下 | |
| B. | 吴圣平对跳板的压力是由于跳板发生形变而产生的 | |
| C. | 吴圣平受到的重力就是它对跳板的压力 | |
| D. | 跳板对吴圣平的支持力是由跳板发生形变而产生的 |
| A. | 2πR,2R | B. | 2R,2πR | C. | 0,2R | D. | 2πR,0 |
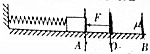 如图所示,轻弹簧一端固定,另一端连接小滑块(可视为质点),在水平外力F作用下,使滑块压缩弹簧至A位置,滑块处于静止状态;现撤去外力F,滑块滑至B处时速度减到零,然后滑块恰好返回O位置时速度再次减为零,O是弹簧原长时滑块的位置(整个过程弹簧始终在弹性限度内),下列说法正确的是( )
如图所示,轻弹簧一端固定,另一端连接小滑块(可视为质点),在水平外力F作用下,使滑块压缩弹簧至A位置,滑块处于静止状态;现撤去外力F,滑块滑至B处时速度减到零,然后滑块恰好返回O位置时速度再次减为零,O是弹簧原长时滑块的位置(整个过程弹簧始终在弹性限度内),下列说法正确的是( )| A. | A到B过程滑块到达O处时有最大速度 | |
| B. | 滑块在B处时加速度为零 | |
| C. | 滑块A到B过程克服摩擦力的功Wf1与B到0过程克服摩擦力的功Wf2的关系为Wf1>2Wf2 | |
| D. | 滑块A到B过程弹簧弹力做的功W1与B到0过程弹簧弹力做的功W2的关系为W1>2W2 |

| A. | 甲与乙的运动方向相同 | B. | 丙与乙的运动方向相同 | ||
| C. | 乙的速度大于甲的速度 | D. | 丙的速率小于乙的速率 |
 某学习小组用伏安法测量一未知电阻Rx的阻值,给定器材及规格为:
某学习小组用伏安法测量一未知电阻Rx的阻值,给定器材及规格为: 如图所示,电源电压E=2V,内阻不计,竖直导轨电阻不计,金属棒的质量m=0.1kg,R=0.5Ω,它与导轨间的动摩擦因数μ=0.4,有效长度为0.2m,靠在导轨外面,为使金属棒不动,施一与纸面夹角37°且垂直于金属棒向里的磁场(g=10m/s2,sin 37°=0.6,cos 37°=0.8).求:(计算结果保留两有效数字)
如图所示,电源电压E=2V,内阻不计,竖直导轨电阻不计,金属棒的质量m=0.1kg,R=0.5Ω,它与导轨间的动摩擦因数μ=0.4,有效长度为0.2m,靠在导轨外面,为使金属棒不动,施一与纸面夹角37°且垂直于金属棒向里的磁场(g=10m/s2,sin 37°=0.6,cos 37°=0.8).求:(计算结果保留两有效数字)