题目内容
19.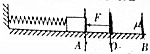 如图所示,轻弹簧一端固定,另一端连接小滑块(可视为质点),在水平外力F作用下,使滑块压缩弹簧至A位置,滑块处于静止状态;现撤去外力F,滑块滑至B处时速度减到零,然后滑块恰好返回O位置时速度再次减为零,O是弹簧原长时滑块的位置(整个过程弹簧始终在弹性限度内),下列说法正确的是( )
如图所示,轻弹簧一端固定,另一端连接小滑块(可视为质点),在水平外力F作用下,使滑块压缩弹簧至A位置,滑块处于静止状态;现撤去外力F,滑块滑至B处时速度减到零,然后滑块恰好返回O位置时速度再次减为零,O是弹簧原长时滑块的位置(整个过程弹簧始终在弹性限度内),下列说法正确的是( )| A. | A到B过程滑块到达O处时有最大速度 | |
| B. | 滑块在B处时加速度为零 | |
| C. | 滑块A到B过程克服摩擦力的功Wf1与B到0过程克服摩擦力的功Wf2的关系为Wf1>2Wf2 | |
| D. | 滑块A到B过程弹簧弹力做的功W1与B到0过程弹簧弹力做的功W2的关系为W1>2W2 |
分析 分析木块的受力情况,刚开始弹力大于摩擦力,先做加速运动,当弹力等于摩擦力时,加速度为零,此时速度最大,后弹力小于摩擦力,滑块做减速运动,弹簧的弹性势能随形变量的减小而减小.根据动能定理分析滑块A到B过程克服摩擦力的功Wf1与B到0过程克服摩擦力的功Wf2的关系以及滑块A到B过程弹簧弹力做的功W1与B到0过程弹簧弹力做的功W2的关系.
解答 解:A、滑块从A到B的过程中,刚开始弹力大于摩擦力,先做加速运动,当弹力等于摩擦力时,加速度为零,此时速度最大,后弹力小于摩擦力,滑块做减速运动,到B速度为零,而O是弹簧原长时滑块的位置,此时弹力为零,不是速度最大的位置,故A错误;
B、滑块在B处时速度为零,弹力大于摩擦力,加速度不为零,故B错误;
C、整个过程中,摩擦力都为滑动摩擦力,大小相等,则克服摩擦力做功W=fx,
从A到B再到O的过程中,根据动能定理得:
0-0=EPA-μmgxAB+BO
从B到C的过程中,根据动能定理得:
0-0=EPB-μmgxBO
而μmgxAB+BO>μmgxBO
所以EPA>EPB,O点弹簧处于原长,则xAO>xBO,所以xAB>2xBO,Wf1=fxAB,Wf2=fxBO,则Wf1>2Wf2,故C正确;
D、从A到B过程,根据动能定理得:0-0=W1-Wf1,从B到O过程,根据动能定理得:0-0=W2-Wf2,而Wf1>2Wf2,则W1>2W2,故D正确.
故选:CD
点评 本题要注意,滑块运动过程中要受到滑动摩擦力作用,不能认为O点是AB的中点,要求同学们能正确分析滑块的运动情况,能结合动能定理求解,难度适中.

练习册系列答案
相关题目
4.如图所示,实践表示其静电场的电场线,虚线表示该电场的等势面.下列判断正确的是( )
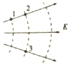

| A. | 1、2两点的场强相等 | |
| B. | 1、3两点的场强相等 | |
| C. | 1、2两点的电势相等 | |
| D. | 把正的试探电荷从1移到2电场力做正功 |
11. 如图所示,小物体分别沿着两个不同的光滑面从静止开始下滑,开始时两物高度相同,滑过的路程相同,则下滑时间( )
如图所示,小物体分别沿着两个不同的光滑面从静止开始下滑,开始时两物高度相同,滑过的路程相同,则下滑时间( )
 如图所示,小物体分别沿着两个不同的光滑面从静止开始下滑,开始时两物高度相同,滑过的路程相同,则下滑时间( )
如图所示,小物体分别沿着两个不同的光滑面从静止开始下滑,开始时两物高度相同,滑过的路程相同,则下滑时间( )| A. | tA>tB | B. | tA<tB | C. | tA=tB | D. | 无法确定 |
9.下列说法中正确的是( )
| A. | 一质点作直线运动,第一秒的位移是1m,第二秒的位移是1m,故此质点作匀速直线运动 | |
| B. | 匀速直线运动是方向不变的运动 | |
| C. | 在任意相同时间内位移相等的运动,一定是匀速直线运动 | |
| D. | 做匀速直线运动的物体的位移和路程相等 |
 如图所示,小滑块在斜面顶端,由静止加速下滑,加速度a=2m/s2,在到达底端前1s内,所滑过的距离为$\frac{13}{49}$L,其中L为斜面长,则
如图所示,小滑块在斜面顶端,由静止加速下滑,加速度a=2m/s2,在到达底端前1s内,所滑过的距离为$\frac{13}{49}$L,其中L为斜面长,则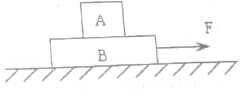 如图,已知重物B的质量为M,A的质量为m,A和B,B与地面间的动摩擦因数都为μ,现在用一水平向右的力F拉物体,使物体一起向右匀加速运动了距离s,求:
如图,已知重物B的质量为M,A的质量为m,A和B,B与地面间的动摩擦因数都为μ,现在用一水平向右的力F拉物体,使物体一起向右匀加速运动了距离s,求: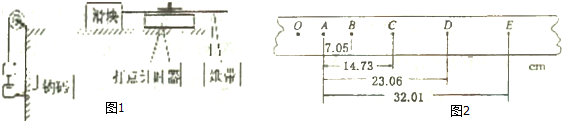
 如图,有3块水平放置的长薄金属板a、b和c,a、b之间相距为L.紧贴b板下表面竖直放置半径为R的半圆形塑料细管,两管口正好位于小孔M、N处.板a与b、b与c之间接有电压可调的直流电源,板b与c间还存在方向垂直纸面向外的匀强磁场.当体积为V0、密度为ρ、电荷量为q的带负电油滴,等间隔地以速率v0从a板上的小孔竖直向下射入,调节板间电压Uba和Ubc,当Uba=U1、Ubc=U2时,油滴穿过b板M孔进入细管,恰能与细管无接触地从N孔射出.忽略小孔和细管对电场的影响,不计空气阻力,重力加速度为g.求:
如图,有3块水平放置的长薄金属板a、b和c,a、b之间相距为L.紧贴b板下表面竖直放置半径为R的半圆形塑料细管,两管口正好位于小孔M、N处.板a与b、b与c之间接有电压可调的直流电源,板b与c间还存在方向垂直纸面向外的匀强磁场.当体积为V0、密度为ρ、电荷量为q的带负电油滴,等间隔地以速率v0从a板上的小孔竖直向下射入,调节板间电压Uba和Ubc,当Uba=U1、Ubc=U2时,油滴穿过b板M孔进入细管,恰能与细管无接触地从N孔射出.忽略小孔和细管对电场的影响,不计空气阻力,重力加速度为g.求: 如图所示,a、b、c、d为匀强电场中四个等势面,相邻等势面间距离为2cm,已知UAC=60V,求:
如图所示,a、b、c、d为匀强电场中四个等势面,相邻等势面间距离为2cm,已知UAC=60V,求: