Question

建筑、桥梁工程中所用的金属材料（如钢筋钢梁等）在外力作用下会伸长，其伸长量不仅与和拉力的大小有关，还和金属材料的横截面积有关．人们发现对同一种金属，其所受的拉力与其横截面积的比值跟金属材料的伸长量与原长的比值的比是一个常数，这个常数叫做杨氏模量．用E表示，即：E=

( F S )

( △L L )

；某同学为探究其是否正确，根据下面提供的器材：不同粗细不同长度的同种金属丝；不同质量的重物；螺旋测微器； 游标卡尺；米尺；天平；固定装置等．设计的实验如图所示．
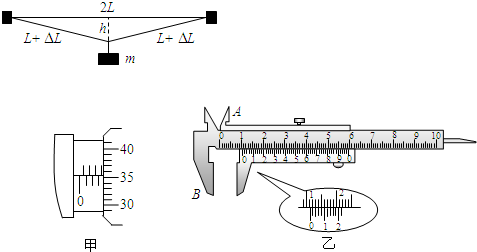
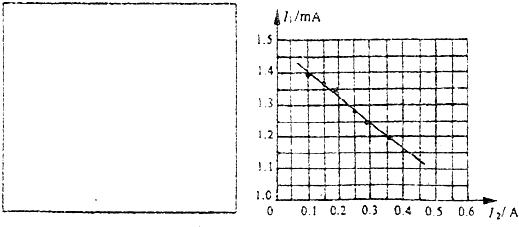
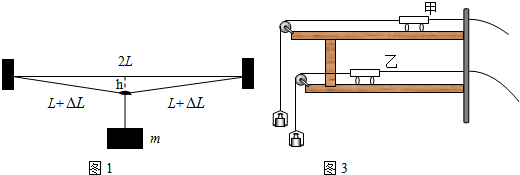
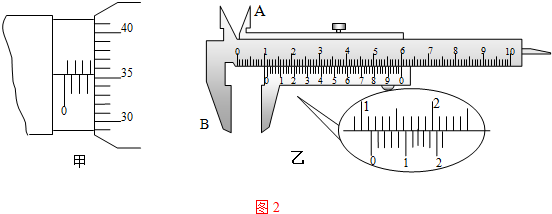
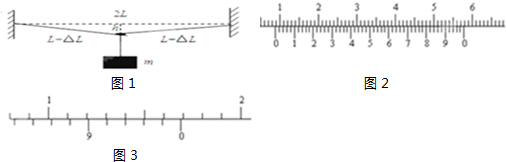
该同学取一段金属丝水平固定在固定装置上，将一重物挂在金属丝的中点，其中点发生了一个微小下移h．用螺旋测微器测得金属丝的直径为D；用游标卡尺测得微小下移量为h；用米尺测得金属丝的原长为2L；用天平测出重物的质量m（不超量程）．
用以上测量量的字母表示该金属的杨氏模量的表达式为：E=

2mgL L2+h2

πD2h( L2+h2-L )

．

Answer 1

分析：根据平衡条件求出金属丝上的拉力，由几何知识求出金属丝的伸长量然后代入公式即可正确解答．

解答：解：由题意可知，根据平衡条件可知，拉伸后金属丝上的拉力为：
F=

mg

2sinθ

，①
由几何关系得：sinθ=

h

L2+h2

②
金属丝的变化量为：△L=L′-2L=

2L

cosθ

③
cosθ=

L

L2+h2

④
横截面积S=

1

4

πD2⑤
联立①②③④⑤解得：E=

( F S )

( △L L )

=

2mgL L2+h2

πD2h( L2+h2-L )

故答案为：

2mgL L2+h2

πD2h( L2+h2-L )

点评：本题属于信息给予题，考查学生获取信息的能力和利用数学知识解决物理问题的能力，是一道考查能力的好题．