题目内容
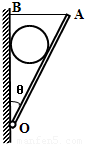
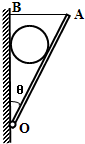 如图所示,光滑均匀球重为G,半径为R,轻板OA长为L,一端用铰链与竖直墙相连于O点,板可绕轴在竖直平面内自由转动,板重可不计,板的A端用一水平细绳AB与墙相连,此时板与竖直墙间的夹角为θ,接触处的摩擦均可不计,如果这一系统保持平衡.试问:
如图所示,光滑均匀球重为G,半径为R,轻板OA长为L,一端用铰链与竖直墙相连于O点,板可绕轴在竖直平面内自由转动,板重可不计,板的A端用一水平细绳AB与墙相连,此时板与竖直墙间的夹角为θ,接触处的摩擦均可不计,如果这一系统保持平衡.试问:(1)竖直墙和轻板对球的弹力分别多大?
(2)细绳对板的拉力F多大?
(3)当θ取何值时,力F有最小值,此最小值多大?
分析:(1)对球受力分析,受重力、挡板支持力N1和墙壁的支持力N2,根据平衡条件列式求解;
(2)以O为支点,对杆有运用力矩平衡条件列式求解;
(3)对拉力F的表达式进行分析,得到拉力的最小值和对应的角度.
(2)以O为支点,对杆有运用力矩平衡条件列式求解;
(3)对拉力F的表达式进行分析,得到拉力的最小值和对应的角度.
解答:解:(1)对球受力分析,受重力、挡板支持力N1和墙壁的支持力N2,如图所示:
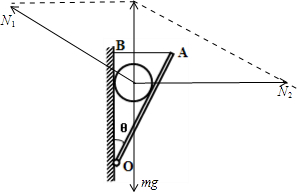
根据平衡条件,有:
N1=
①
N2=Gcotθ ②
(2)以O为支点,杆受球的压力和细线的拉力,根据力矩平衡条件,有:
F?Lcosθ=N1?R?cot
③
由①③联立解得:F=
④
(3)由④式,当cosθ=1-cosθ,即θ=60°时,拉力F有最小值,为
;
答:(1)竖直墙对球的弹力为Gcotθ,轻板对球弹力为
;
(2)细绳对板的拉力F为
;
(3)当θ取60°时,力F有最小值,此最小值为
.

根据平衡条件,有:
N1=
| G |
| sinθ |
N2=Gcotθ ②
(2)以O为支点,杆受球的压力和细线的拉力,根据力矩平衡条件,有:
F?Lcosθ=N1?R?cot
| θ |
| 2 |
由①③联立解得:F=
| GR |
| Lcosθ(1-cosθ) |
(3)由④式,当cosθ=1-cosθ,即θ=60°时,拉力F有最小值,为
| 4GR |
| L |
答:(1)竖直墙对球的弹力为Gcotθ,轻板对球弹力为
| G |
| sinθ |
(2)细绳对板的拉力F为
| GR |
| Lcosθ(1-cosθ) |
(3)当θ取60°时,力F有最小值,此最小值为
| 4GR |
| L |
点评:本题关键是根据共点力平衡条件和力矩平衡条件列式求解,对应极值问题,关键是要根据数学中的表达式知识求解.

练习册系列答案
相关题目
 如图所示,质量均匀的光滑球夹在斜面与木板之间,木板可绕连接斜面的轴转动,在木板绕铰链的水平轴转动的过程中( )
如图所示,质量均匀的光滑球夹在斜面与木板之间,木板可绕连接斜面的轴转动,在木板绕铰链的水平轴转动的过程中( ) (2012?黄埔区模拟)如图所示,质量均匀的球夹在光滑竖直墙面和光滑轻板之间,轻板可绕其L端的水平轴O自由转动.在轻板上端用竖直向上的拉力F提着轻板,使其缓慢放下,直到轻板呈水平之前,F的大小以及F对于轴O的力矩M的大小变化情况是( )
(2012?黄埔区模拟)如图所示,质量均匀的球夹在光滑竖直墙面和光滑轻板之间,轻板可绕其L端的水平轴O自由转动.在轻板上端用竖直向上的拉力F提着轻板,使其缓慢放下,直到轻板呈水平之前,F的大小以及F对于轴O的力矩M的大小变化情况是( )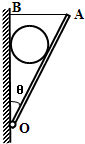 如图所示,光滑均匀球重为G,半径为R,轻板OA长为L,一端用铰链与竖直墙相连于O点,板可绕轴在竖直平面内自由转动,板重可不计,板的A端用一水平细绳AB与墙相连,此时板与竖直墙间的夹角为θ,接触处的摩擦均可不计,如果这一系统保持平衡.试问:
如图所示,光滑均匀球重为G,半径为R,轻板OA长为L,一端用铰链与竖直墙相连于O点,板可绕轴在竖直平面内自由转动,板重可不计,板的A端用一水平细绳AB与墙相连,此时板与竖直墙间的夹角为θ,接触处的摩擦均可不计,如果这一系统保持平衡.试问: