题目内容
6.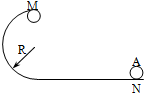 如图,半径为R=20cm的竖直放置的圆轨道与水平直轨道相连接,质量为m=50g的小球A以一定的初速度由直轨道向左运动,并沿圆轨道的内壁冲上去,如果A经过N点时的速度v1=4m/s,A恰能经过轨道最高点M,取g=10m/s2.求:
如图,半径为R=20cm的竖直放置的圆轨道与水平直轨道相连接,质量为m=50g的小球A以一定的初速度由直轨道向左运动,并沿圆轨道的内壁冲上去,如果A经过N点时的速度v1=4m/s,A恰能经过轨道最高点M,取g=10m/s2.求:(1)小球A从N到M这一段过程中克服阻力做的功W.
(2)小球A从M落到水平直轨道上水平方向上通过的位移.
分析 (1)A恰能经过轨道最高点M,则小球经过M点时,由重力的合力提供向心力,根据牛顿第二定律可求出小球经过M点的速度;再对N到M过程,运用动能定理求克服阻力做的功W.
(2)小球离开M点后做平抛运动,根据分位移公式求解水平位移.
解答 解:(1)在M点,由牛顿第二定律得
mg=m$\frac{{v}_{M}^{2}}{R}$
得 vM=$\sqrt{gR}$=$\sqrt{10×0.2}$=$\sqrt{2}$m/s
对于N到M过程,运用动能定理得
-mg•2R-W=$\frac{1}{2}m{v}_{M}^{2}$-$\frac{1}{2}m{v}_{1}^{2}$
解得,W=0.15J
(2)小球离开M点后做平抛运动,则
2R=$\frac{1}{2}g{t}^{2}$
x=vMt
解得 x=vM$\sqrt{\frac{4R}{g}}$=$\sqrt{2}$×$\sqrt{\frac{4×0.2}{10}}$=0.4m
答:
(1)小球A从N到M这一段过程中克服阻力做的功W为0.15J.
(2)小球A从M落到水平直轨道上水平方向上通过的位移是0.4m.
点评 本题是动能定理与向心力、平抛运动知识的综合应用.题中阻力是变力,要学会运用动能定理求变力做功.

练习册系列答案
相关题目
16. 如图所示是一个简易起吊设施的示意图,AC是撑杆,质量不计,C端与竖直墙用铰链连接,一滑轮固定在A点正上方,现施一拉力F缓慢将重物P上拉,在AC杆达到竖直前( )
如图所示是一个简易起吊设施的示意图,AC是撑杆,质量不计,C端与竖直墙用铰链连接,一滑轮固定在A点正上方,现施一拉力F缓慢将重物P上拉,在AC杆达到竖直前( )
 如图所示是一个简易起吊设施的示意图,AC是撑杆,质量不计,C端与竖直墙用铰链连接,一滑轮固定在A点正上方,现施一拉力F缓慢将重物P上拉,在AC杆达到竖直前( )
如图所示是一个简易起吊设施的示意图,AC是撑杆,质量不计,C端与竖直墙用铰链连接,一滑轮固定在A点正上方,现施一拉力F缓慢将重物P上拉,在AC杆达到竖直前( )| A. | 绳上拉力F越来越大 | B. | 绳上中拉力F越来越小 | ||
| C. | AC杆中的支撑力FN越来越大 | D. | AC杆中的支撑力FN不变 |
1. 在水平转动的圆台上放有甲、乙两个小物体,当圆台绕其中心的竖直轴OO′转动时,两个小物体随圆台一起转动,如图所示,两物体与圆台平面间的动摩擦因素相同,那么当圆台转速增大时,以下说法正确的是( )
在水平转动的圆台上放有甲、乙两个小物体,当圆台绕其中心的竖直轴OO′转动时,两个小物体随圆台一起转动,如图所示,两物体与圆台平面间的动摩擦因素相同,那么当圆台转速增大时,以下说法正确的是( )
 在水平转动的圆台上放有甲、乙两个小物体,当圆台绕其中心的竖直轴OO′转动时,两个小物体随圆台一起转动,如图所示,两物体与圆台平面间的动摩擦因素相同,那么当圆台转速增大时,以下说法正确的是( )
在水平转动的圆台上放有甲、乙两个小物体,当圆台绕其中心的竖直轴OO′转动时,两个小物体随圆台一起转动,如图所示,两物体与圆台平面间的动摩擦因素相同,那么当圆台转速增大时,以下说法正确的是( )| A. | 甲物体先滑动 | B. | 乙物体先滑动 | ||
| C. | 两物体同时滑动 | D. | 甲乙的质量未知,无法确定 |
15.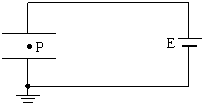 如图所示,平行板电容器与电动势为E的直流电源(内阻不计)连接,下极板接地.一带电油滴位于容器中的P点且恰好处于平衡状态.现将平行板电容器的上极板竖直向上移动一小段距离( )
如图所示,平行板电容器与电动势为E的直流电源(内阻不计)连接,下极板接地.一带电油滴位于容器中的P点且恰好处于平衡状态.现将平行板电容器的上极板竖直向上移动一小段距离( )
 如图所示,平行板电容器与电动势为E的直流电源(内阻不计)连接,下极板接地.一带电油滴位于容器中的P点且恰好处于平衡状态.现将平行板电容器的上极板竖直向上移动一小段距离( )
如图所示,平行板电容器与电动势为E的直流电源(内阻不计)连接,下极板接地.一带电油滴位于容器中的P点且恰好处于平衡状态.现将平行板电容器的上极板竖直向上移动一小段距离( )| A. | 油滴带负电 | |
| B. | 带点油滴将沿竖直方向向上运动 | |
| C. | P的电势将降低 | |
| D. | 电容器的电容减小,而极板带电量将增大 |

 真空管经常用来做羽毛和铜钱同时下落的实验,如图,真空管的质量为0.6千克,长度为1米,置于管顶的铜钱质量为 0.05千克,可以视为质点,管底离地面0.2米
真空管经常用来做羽毛和铜钱同时下落的实验,如图,真空管的质量为0.6千克,长度为1米,置于管顶的铜钱质量为 0.05千克,可以视为质点,管底离地面0.2米 如图,在倾角为θ的光滑斜面上,放一个重为G的球A,球A被竖直挡板K挡住.则球A对竖直挡板的压力大小为多少?球对斜面的压力大小为多少?
如图,在倾角为θ的光滑斜面上,放一个重为G的球A,球A被竖直挡板K挡住.则球A对竖直挡板的压力大小为多少?球对斜面的压力大小为多少? 如图所示,质量m=2kg 的物体在恒定的水平推力F作用下,从固定斜面的底端由静止开始沿斜面向上运动,已知斜面的倾角θ=37°,物体与斜面间的动摩擦因数μ=0.5.若已知F=42N,设斜面足够长(g 取10m/s2)求:
如图所示,质量m=2kg 的物体在恒定的水平推力F作用下,从固定斜面的底端由静止开始沿斜面向上运动,已知斜面的倾角θ=37°,物体与斜面间的动摩擦因数μ=0.5.若已知F=42N,设斜面足够长(g 取10m/s2)求: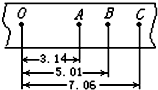 在“验证机械能守恒定律”的实验中,打点周期为0.02s,自由下落的重物质量为1kg,打出一条理想的纸带,数据如图所示,单位是cm,g取10m/s2,O、A之间有多个点没画出.
在“验证机械能守恒定律”的实验中,打点周期为0.02s,自由下落的重物质量为1kg,打出一条理想的纸带,数据如图所示,单位是cm,g取10m/s2,O、A之间有多个点没画出.