题目内容
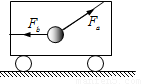
在静止的小车内，用细绳a和b系住一个小球．绳a与竖直方向成θ角，拉力为Ta，绳b成水平状态，拉力为Tb．现让小车从静止开始向右做匀加速直线运动，如图所示．此时小球在车内的位置仍保持不变（角θ不变）．则两根细绳的拉力变化情况是（ ）分析：对静止状态和匀加速状态分别受力分析，求出两个绳子拉力的表达式，再对结果讨论即可．
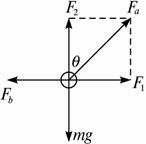
解答：解：物体以加速度a向右做匀加速直线运动，对小球受力分析，如图
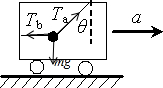
根据共点力平衡条件
Tasinθ-Tb=ma
Tacosθ-mg=0
解得
Ta=
Tb=mgtanθ-ma
故当物体由静止开始加速时，加速度由零变为不是零，即变大，故Ta不变，Tb变小；
故选D．
根据共点力平衡条件
Tasinθ-Tb=ma
Tacosθ-mg=0
解得
Ta=
| mg |
| cosθ |
Tb=mgtanθ-ma
故当物体由静止开始加速时，加速度由零变为不是零，即变大，故Ta不变，Tb变小；
故选D．
点评：本题关键是对小球受力分析，根据牛顿第二定律列出方程求解出各个力的表达式，然后进行讨论．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
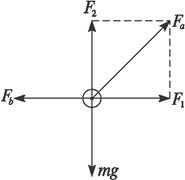
（2009?东城区模拟）在静止的小车内，用细绳a和b系住一个小球，绳a处于斜向上的方向，拉力为Fa，绳b处于水平方向，拉力为Fb，如图所示．现让小车从静止开始向右做匀加速运动，此时小球相对于车厢的位置仍保持不变，则两根细绳的拉力变化情况是（ ）
