题目内容
18. 如图所示,轻弹簧左端固定在水平地面的N点处,弹簧自然伸长时另一端位于O点,水平面NO段为光滑地面,B点右侧为粗糙水平面,O点和M点的距离为L,现有质量相等均为m的A、B滑块,先用滑块B向左压缩弹簧至P点,B和弹簧不栓接,由静止释放后向右运动与静止在M点的A物体碰撞,碰撞后A与B粘在一起,A向右运动了L之后静止在水平面上,已知水平面与滑块之间滑动摩擦因数都为μ,求
如图所示,轻弹簧左端固定在水平地面的N点处,弹簧自然伸长时另一端位于O点,水平面NO段为光滑地面,B点右侧为粗糙水平面,O点和M点的距离为L,现有质量相等均为m的A、B滑块,先用滑块B向左压缩弹簧至P点,B和弹簧不栓接,由静止释放后向右运动与静止在M点的A物体碰撞,碰撞后A与B粘在一起,A向右运动了L之后静止在水平面上,已知水平面与滑块之间滑动摩擦因数都为μ,求(1)B刚与A碰撞后,A的速度大小?
(2)B将弹簧压缩至P点时克服弹力所做的功?
(3)若将B物体换成质量是2m的C物体,其余条件不变,则求A向右运动的距离是多少?
分析 (1)对AB系统,由动能定理可以求出其速度.
(2)AB碰撞过程系统动量守恒,应用动量守恒定律与能量守恒定律可以求出功.
(3)碰撞过程动量守恒,应用动量守恒定律与动能定理可以求出滑行的距离
解答 解:(1)对碰后,对物体A和B,由动能定理得:
$\frac{1}{2}2mV_1^2=2μmgL$,
解得:$V_1^{\;}=\sqrt{2μgL}$;
(2)A和B碰撞过程系统守恒,以向右为正方向,由动量守恒定律得:mv2=2mv1
从O到M点过程,由动能定理得:$\frac{1}{2}mV_2^2-\frac{1}{2}mV_3^2=-μmgL$
克服弹力做的功:W=$\frac{1}{2}mV_3^2$=5μmgL;
(3)对C物体:W=$\frac{1}{2}2mV_4^2$
C物体从O到M点由动能定理:$\frac{1}{2}2mV_5^2-\frac{1}{2}2mV_4^2=-2μmgL$
C和A碰撞过程系统动量守恒,以向右为正方向,由动量守恒定律得:2mv5=3mv6
对碰后物体A和C由动能定理:$\frac{1}{2}3mV_6^2=3μmgx$,
解得:$x=\frac{2L}{3}$;
答:(1)B刚与A碰撞后,A的速度大小为$\sqrt{2μgL}$;
(2)B将弹簧压缩至P点时克服弹力所做的功为5μmgL;
(3)若将B物体换成质量是2m的C物体,其余条件不变,A向右运动的距离是$\frac{2}{3}$L.
点评 本题考查了求速度、功与物体滑行距离问题,分析清楚物体运动过程、应用动能定理、动量守恒定律、能量守恒定律即可正确解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.关于电磁波的应用,下列说法正确的是( )
| A. | 医院里常用X射线对手术室进行消毒 | |
| B. | 工业上利用γ射线检查金属内部有无沙眼 | |
| C. | 利用红外线遥感技术在卫星上监测森林火情 | |
| D. | 利用紫外线烘干谷物 |
9.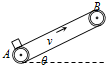 某机场利用如图所示的传送带将地面上的货物运送到飞机上,传送带与地面的夹角θ=30°传送带两端A、B的长度L=10m.传送带以v=5m/s的恒定速度匀速向上运动.在传送带底端A轻轻放一质量m=5kg的货物,货物与传送带间的动磨擦因数为$\frac{\sqrt{3}}{2}$,g取10m/s2.( )
某机场利用如图所示的传送带将地面上的货物运送到飞机上,传送带与地面的夹角θ=30°传送带两端A、B的长度L=10m.传送带以v=5m/s的恒定速度匀速向上运动.在传送带底端A轻轻放一质量m=5kg的货物,货物与传送带间的动磨擦因数为$\frac{\sqrt{3}}{2}$,g取10m/s2.( )
 某机场利用如图所示的传送带将地面上的货物运送到飞机上,传送带与地面的夹角θ=30°传送带两端A、B的长度L=10m.传送带以v=5m/s的恒定速度匀速向上运动.在传送带底端A轻轻放一质量m=5kg的货物,货物与传送带间的动磨擦因数为$\frac{\sqrt{3}}{2}$,g取10m/s2.( )
某机场利用如图所示的传送带将地面上的货物运送到飞机上,传送带与地面的夹角θ=30°传送带两端A、B的长度L=10m.传送带以v=5m/s的恒定速度匀速向上运动.在传送带底端A轻轻放一质量m=5kg的货物,货物与传送带间的动磨擦因数为$\frac{\sqrt{3}}{2}$,g取10m/s2.( )| A. | 货物从A到B过程中摩擦力不变 | B. | 货物从A到B的时间为3s | ||
| C. | 货物传送带上滑动的时间为2s | D. | 货物相对传送带滑动的距离为5m |
6.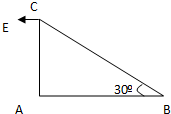 如图,A、B、C三点为一直角三角形的三个顶点,∠B=30°,现在A、B两点放置两点电荷qA、qB,测得C点场强方向与BA平行,则关于qA、qB的电性及其大小关系,下列说法中正确的是( )
如图,A、B、C三点为一直角三角形的三个顶点,∠B=30°,现在A、B两点放置两点电荷qA、qB,测得C点场强方向与BA平行,则关于qA、qB的电性及其大小关系,下列说法中正确的是( )
 如图,A、B、C三点为一直角三角形的三个顶点,∠B=30°,现在A、B两点放置两点电荷qA、qB,测得C点场强方向与BA平行,则关于qA、qB的电性及其大小关系,下列说法中正确的是( )
如图,A、B、C三点为一直角三角形的三个顶点,∠B=30°,现在A、B两点放置两点电荷qA、qB,测得C点场强方向与BA平行,则关于qA、qB的电性及其大小关系,下列说法中正确的是( )| A. | qA一定带正电 | B. | qB一定带正电 | C. | qA:qB=1:4 | D. | qA:qB=1:8 |
10. 如图所示,线段A为某电源的U-I图线,线段B为某电阻的U-I图线,将上述电源和电阻组成闭合电路时,下列说法正确的是( )
如图所示,线段A为某电源的U-I图线,线段B为某电阻的U-I图线,将上述电源和电阻组成闭合电路时,下列说法正确的是( )
 如图所示,线段A为某电源的U-I图线,线段B为某电阻的U-I图线,将上述电源和电阻组成闭合电路时,下列说法正确的是( )
如图所示,线段A为某电源的U-I图线,线段B为某电阻的U-I图线,将上述电源和电阻组成闭合电路时,下列说法正确的是( )| A. | 电阻B的阻值为1Ω | B. | 电源的总功率为5W | ||
| C. | 电源的输出功率为4W | D. | 电源的效率为50% |
7.简谐横波某时刻的波形图线如图所示,a为介质中的一个质点,由图象可知( )
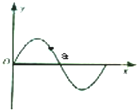

| A. | 此时质点a的加速度方向一定沿y轴负方向 | |
| B. | 此时质点a的速度方向一定沿y轴负方向 | |
| C. | 若波向左传播,则此时a的速度方向一定沿y轴负方向 | |
| D. | 若波向右传播,则此时a的速度方向一定沿y轴负方向 |
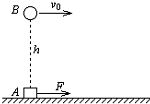 如图所示,质量m=2kg的物体A在水平恒力F的作用下由静止开始沿水平面向右运动,同时在物体A的正上方相距h=20cm高处,有一物体B正以初速度v0水平向右抛出.在物体A发生了s=80cm位移时恰好被B物体击中,取g=10m/s2,试求:
如图所示,质量m=2kg的物体A在水平恒力F的作用下由静止开始沿水平面向右运动,同时在物体A的正上方相距h=20cm高处,有一物体B正以初速度v0水平向右抛出.在物体A发生了s=80cm位移时恰好被B物体击中,取g=10m/s2,试求: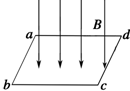 如图所示,矩形线圈有N匝,面积大小为S,放在水平面内,加一个竖直向下的范围较大的匀强磁场,磁感应强度为B,则穿过平面的磁通量是多少?若使线圈绕ab边转过60°,则穿过线圈平面的磁通量是多少?
如图所示,矩形线圈有N匝,面积大小为S,放在水平面内,加一个竖直向下的范围较大的匀强磁场,磁感应强度为B,则穿过平面的磁通量是多少?若使线圈绕ab边转过60°,则穿过线圈平面的磁通量是多少?