题目内容

3．速度、加速度的测量通常比位移的测量要复杂些，而有时我们只需比较两个物体运动的加速度，并不需要知道加速度的大小，例如比较两辆汽车的加速性能就是这样，若已知两辆汽车由静止开始做匀加速直线运动，在相同时间内两车的位移之比为2：1，则它们的加速度之比为（　　）
A．1：2B．1：4C．2：1D．4：1

分析 初速度为零的匀加速直线运动，根据x=$\frac{1}{2}a{t}^{2}$，抓住时间相等，求出加速度之比．

解答 解：根据x=$\frac{1}{2}a{t}^{2}$得：a=$\frac{2x}{{t}^{2}}$，由于时间相等，位移之比为2：1，则加速度之比为2：1．故C正确，ABD错误．
故选：C．

点评 解决本题的关键掌握匀变速直线运动的位移时间公式，并能灵活运用，基础题．

练习册系列答案
相关题目
13．一质点做匀加速直线运动时，速度变化△v时发生位移x1，紧接着速度变化同样的△v时发生位移x2，则该质点的加速度为（　　）
A．（△v）2（$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$）B．2$\frac{（△v）^{2}}{{x}_{1}-{x}_{2}}$C．（△v）2（$\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$）D．$\frac{（△v）^{2}}{{x}_{1}-{x}_{2}}$
14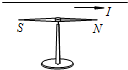．如图所示，把一条导线平行地放在磁针的上方附近，当电流通过导线时，磁针会发生偏转．首先观察到这个实验现象的物理学家是（　　）
A．奥斯特B．爱因斯坦C．法拉第D．欧姆
11．厦门六中985课题研究小组，收集了数码相机、手机等用旧了的各种类型的电池，及从废旧收音机上拆下的电阻、电容、电感线圈、薄的金属圆片．现从这些材料中选取两个待测元件，一是手机中常用的锂电池（电动势E标称值为3.7V，允许最大放电电流为100mA）．二是薄的金属圆片．在操作台上还准备了如下实验器材：
A．电压表V1（量程4V，电阻RV约为5.0kΩ），
B．电压表V2（量程15V，电阻RV约为20.0kΩ），
C．电流表A1（量程100mA，电阻RA1约为10Ω），
D．电流表A2（量程4mA，电阻RA2约为50Ω），
E．滑动变阻器R1（0～20Ω，额定电流1A），
F．滑动变阻器R2（0～2000Ω，额定电流3A）
G．开关S一只、导线若干，
H．游标卡尺，
I．螺旋测微器．
（1）为了测锂电池的电动势和内阻，课题组某成员设计出了实验原理图1，请你指出其中的错误（只要求写出2条）：应选电流表A1；电压表选择V1．

（2）课题组某成员根据测得的数据，在U-I图2中描出了数据点，请你根据图中的点求出该锂电池的内阻r=21.7Ω．
（3）课题组某成员用游标卡尺和螺旋测微器分别测量薄金属圆片的直径和厚度．请你读出图3中的示数．该游标卡尺示数为1.240cm．螺旋测微器示数为0.730mm．
18．双层巴士靠站后，没有下车的乘客，因下层坐满了乘客，驾驶员提醒上层的后面有空位，新上车的乘客走向上层的后方入座，此时车（包括乘客）的重心（　　）
A．向前上方移动B．向后上方移动C．向上移动D．不变
8．甲乙两车在一平直道路上同向运动，其v-t图象如图所示，图中△OPQ、△OQT的面积分别为s1和s2（s2＞s1）．初始时，甲车在乙车前方s0处，下列说法正确的是（　　）
A．不论怎样，两车一定至少相遇1次B．若s0＜s1，两车一定相遇2次
C．若s0＜s2，两车一定相遇2次D．若s0=s2，两车一定相遇1次
15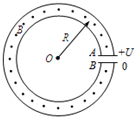．如图所示为一种获得高能粒子的装置，由光滑绝缘材料围成的环形区域内存在垂直纸面向外、磁感应强度大小为B的均匀磁场（环形区域的宽度非常小）．质量为m、电荷量为+q的粒子可在环中做半径为R的圆周运动．A、B为两块中心开有小孔的距离很近的极板，原来电势均为零，每当带电粒子经过A板准备进入AB之间时，A板电势升高为+U，B板电势仍保持为零，粒子在两板间的电场中得到加速．每当粒子离开B板时，A板电势又降为零．粒子在电场中一次次加速下动能不断增大，而在环形磁场中绕行半径R不变．（设极板间距远小于R）下列说法正确的是（　　）
A．粒子从A板小孔处由静止开始在电场力作用下加速，绕行N圈后回到A板时获得的总动能为NqU
B．粒子在绕行的整个过程中，每一圈的运动时间为$\frac{2πm}{Bq}$
C．粒子获得的最大速度与加速次数无关，由R决定
D．粒子绕行第N圈时所受向心力为$\frac{2NUq}{R}$
12．物理兴趣小组的同学们从实验室中找到一只小灯泡，其标称功率值为0.75W，额定电压值已模糊不清．他们想测定其额定电压值，于是先用欧姆表直接测出该灯泡的电阻约为2Ω，然后根据公式计算出该灯泡的额定电压U=$\sqrt{PR}$=$\sqrt{2×0.75}$ V=1.22V．他们怀疑所得电压值不准确，于是，再利用下面可供选择的实验器材设计一个电路，测量通过灯泡的电流和它两端的电压．根据测量数据已绘出灯泡的U-I图象，如图1所示．
A．电压表V（量程3V，内阻约3kΩ）
B．电流表A1（量程150mA，内阻约2Ω）
C．电流表A2（量程500mA，内阻约0.6Ω）
D．滑动变阻器R1（0～20Ω）
E．滑动变阻器R2（0～100Ω）
F．电源E（电动势4.0V，内阻不计）
H．开关S和导线若干
G．待测灯泡L（额定功率0.75W，额定电压未知）

（1）在下面所给定的图2虚线框中画出他们进行实验的电路原理图，指出上述器材中，电流表选择A2（填“A1”或“A2”）；滑动变阻器选择R1（填“R1”或“R2”）．
（2）从图象上分析该灯泡的额定电压应为2.5V；这一结果大于开始时的计算结果，原因是灯泡冷态电阻小于正常工作时的电阻．
13．图甲为一台小型发电机构造示意图，内阻r=5.0Ω，外电路电阻R=95Ω，电路中其余电阻不计．发电机内的矩形线圈在匀强磁场中以恒定的角速度ω绕垂直于磁场方向的固定轴转动，线圈匝数n=100．转动过程中穿过每匝线圈的磁通量Φ随时间t按正弦规律变化，如图乙所示，则（　　）
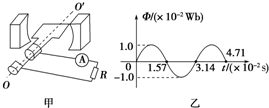
A．t=3.14×10-2 s时，该小型发电机的电动势为零
B．该小型发电机的电动势的最大值为200 V
C．电路中电流最大值为2 A
D．串联在外电路中的交流电流表的读数为2 A

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网