题目内容
如图所示，ACB是一光滑的、足够长的固定在竖直平面内的“∧”形框架，其中CA、CB边与竖直方向的夹角分别为α=37°，β=53°，P、Q两个轻质小环分别套在CA、CB上，两根细绳的一端分别系在P、Q环上，另一端和一绳套系在一起，结点为O．将质量为m的钩码挂在绳套上，OP、OQ两根细绳拉直后的长度分别用l1、l2表示，若l1：l2=2：3，已知sin37°=0.6，则两绳受到的拉力之比F1：F2等于（ ）分析：先对PQ环受力分析，它们只受两个力，根据二力平衡条件可知，绳子的拉力都是垂直于杆子的，这是解决此题的关键．再对结点O受力分析，再根据三力平衡求解F1：F2．
解答：解：对P、Q小环分析，小环受光滑杆的支持力和绳子的拉力，根据平衡条件，这两个力是一对平衡力，支持力是垂直于杆子向上的，故绳子的拉力也是垂直于杆子的．
对结点O受力分析如图所示．
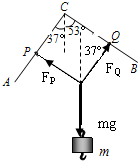
根据平衡条件可知，FP和FQ的合力与mg等值反向，如图所示．几何关系可知，
故FP：FQ=tan37°：1=sin37°：sin53°=3：4
故选A．
对结点O受力分析如图所示．
根据平衡条件可知，FP和FQ的合力与mg等值反向，如图所示．几何关系可知，
故FP：FQ=tan37°：1=sin37°：sin53°=3：4
故选A．
点评：本题的解题关键是抓住两环只受两个力，二力平衡，确定出两绳的方向．还要能正确的受力分析，并且能熟练运用几何知识分析力的关系；题中绳子长度之比是干扰条件．
练习册系列答案
相关题目
（2009?徐州二模）如图所示，ACB是一光滑的、足够长的、固定在竖直平面内的“∧”形框架，其中CA、CB边与竖直方向的夹角均为θ．P、Q两个轻质小环分别套在CA、CB上，两根细绳的一端分别系在P、Q环上，另一端和一绳套系在一起，结点为O．图中虚线为竖直线，将质量为m的钩码挂在绳套上，OP、OQ两根细绳拉直后的长度分别用l1、l2表示，若l1：l2=2：3，则两绳受到的拉力之比F1：F2等于（ ）
如图所示，ACB是一光滑的、足够长的、固定在竖直平面内的“∧”形框架，其中CA、CB边与竖直方向的夹角为θ．P、Q两个轻质小环分别套在CA、CB上，两根细绳的一端分别系在P、Q环上，另一端和一绳套系在一起，结点为O．OP、OQ两根细绳的长度分别l1、l2表示，长度之l1：l2=2：3，那么将质量为m的钩码挂在该绳套上，则两绳受到的拉力之比F1：F2等于（ ）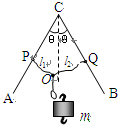
如图所示，ACB是一光滑的、足够长的、固定在竖直平面内的“∧”形框架，其中CA、CB边与竖直方向的夹角均为θ=37°．P、Q两个轻质小环分别套在CA、CB上，两根细绳的一端分别系在P、Q环上，另一端和一绳套系在一起，结点为O．将质量为m的钩码挂在绳套上，OP、OQ两根细绳拉直后的长度分别用l1、l2表示，受到的拉力分别用F1和F2表示．若l1=l2，则两绳受到的拉力F1=F2=
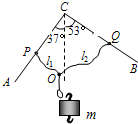如图所示，ACB是一光滑的、足够长的、固定在竖直平面内的“∧”形框架，其中CA、CB边与竖直方向的夹角分别为37°和53°．P、Q两个轻质小环分别套在CA、CB上，两根细绳的一端分别系在P、Q环上，另一端和一绳套系在一起，结点为O．将质量为m的钩码挂在绳套上，OP、OQ两根细绳拉直后的长度分别用l1、l2表示，受到的拉力分别用F1和F2表示，则（ ）