题目内容
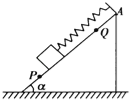
【题目】如图所示，在倾角α=60°的斜面上，放一质量为10kg的物体，用k=100N/m的轻质弹簧平行于斜面拉着，物体放在PQ之间任何位置都能处于静止状态，而超过这一范围，物体就会沿斜面滑动，若AP=22cm，AQ=8cm，试求物体与斜面间的最大静摩擦力的大小？（sin60°=
，cos60°=
）
【答案】7N
【解析】试题分析：由题，当物体位于P点时，将要向上运动，静摩擦力沿斜面向下达到最大．当物体位于Q点时，物体将向下运动，静摩擦力沿斜面向上达到最大．根据平衡条件和胡克定律列方程求解最大静摩擦力．
解：P、Q两点应是静摩擦力最大的两个临界位置，在P点弹簧处于伸长状态，受力分析如图（1）所示．Ffm=F1﹣mgsinα ①
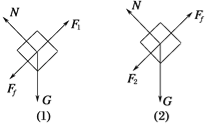
在Q点弹簧处于压缩状态，受力分析如图（2）所示．
Ffm=F2+mgsinα ②
设弹簧的原长为x，有F1=k（0.22﹣x） ③
F2=k（x﹣0.08） ④
联立①②③④得：2Ffm=F1+F2=k（0.22﹣0.08）
所以Ffm=
×100×0.14 N="7" N
答：物体与斜面间的最大静摩擦力的大小是7N．
练习册系列答案
全能测控期末小状元系列答案
相关题目
