��Ŀ����
����Ŀ����ͼ��ʾ��һ��С����v0=8.0m/s�ٶȴ�Բ�������O��ˮƽ�׳���ǡ��������б�����ڵķ���ƽ����б������Q�㣮��֪б��⻬��б����ˮƽ��ļн�Ϊ��=37�㣬б��ĸ߶�Ϊh=15m�����Կ���������Ӱ�죬�������ٶ�Ϊg=10m/s2 �� ����֪sin37��=0.6��co37��=0.8��tan37��=0.75������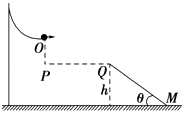
��1�����׳�������Q�����õ�ʱ���Լ�����Q��ʱ�ٶȵĴ�С��
��2��С���O���׳����˶���б��˵�M�����õ���ʱ�䣨���������λ��Ч���֣���
���𰸡�
��1���⣺��С���O��Q���õ�ʱ��Ϊt1����ƽ���˶����ɵã�
��Ϊ tan��= ![]()
���� t1=0.6s
�䵽Q����ٶ�Ϊ��v= ![]() =
= ![]() =10m/s��
=10m/s��
�𣺴��׳�������Q�����õ�ʱ����0.6s������Q��ʱ�ٶȵĴ�С��10m/s��
��2���⣺��С����б�����˶��ļ��ٶ�Ϊa��ʱ��Ϊt2��
����a= ![]() =gsin��=6m/s2
=gsin��=6m/s2
��б���»���λ�� x= ![]() =
= ![]() m=25m
m=25m
��x=vt2+ ![]() �������ݽ�ã�t2��1.7 s
�������ݽ�ã�t2��1.7 s
����С���O���׳���б��˵�M�����õ���ʱ��Ϊ��t=t1+t2��2.3 s��
��С���O���׳����˶���б��˵�M�����õ���ʱ����2.3s��
����������1��С���O���׳�����ƽ���˶�������ƽ���˶��Ĺ��ɣ���ʽ��⡣
��2��С���O���׳����˶��ֳ��������̣�����ƽ���˶�Ȼ�����ȼ����˶����ֱ���ݹ�����ʽ��⼴�ɡ�

 ��У����ϵ�д�
��У����ϵ�д�