题目内容
19. 如图,三棱镜的横截面为直角三角形ABC,∠A=30°,∠B=60°,BC边长度为L,一束垂直于AB边的光线自AB边的P点射入三棱镜,AP长度d<L,光线在AC边同时发生反射和折射,反射光线和折射光线恰好相互垂直,已知光在真空中的速度为c,求:
如图,三棱镜的横截面为直角三角形ABC,∠A=30°,∠B=60°,BC边长度为L,一束垂直于AB边的光线自AB边的P点射入三棱镜,AP长度d<L,光线在AC边同时发生反射和折射,反射光线和折射光线恰好相互垂直,已知光在真空中的速度为c,求:(1)三棱镜的折射率;
(2)光从P点射入到第二次射出三棱镜经过的时间.
分析 (1)光线射到AC边上的O点,由折射定律和几何关系求三棱镜的折射率.
(2)光线反射到AB边上,由几何关系求出入射角,与临界角比较,能发生全反射.再反射从BC边射出.由v=$\frac{c}{n}$求出光在棱镜中传播的速度,由几何关系求出传播的距离,再求传播时间.
解答 解:(1)光线到达AC边的O点,入射角为i,折射角为r.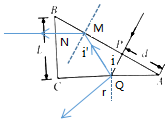
由题意可得:i+r=90°
i=30°
所以 r=60°
可得三棱镜的折射率 n=$\frac{sinr}{sini}$=$\frac{sin60°}{sin30°}$=$\sqrt{3}$
(2)光线反射到AB边的M点,入射角为 i′=60°
因为 sini′=$\frac{\sqrt{3}}{2}$>$\frac{1}{n}$=sinC,得 i′>C,所以光线在M点发生全反射,不会射出三棱镜.
PQ=dtan30°=$\frac{\sqrt{3}}{3}$d
QM=2PQ
MN=($\frac{L}{sin30°}$-2d)cos30°=$\sqrt{3}$(L-d)
光在三棱镜中传播速度为:v=$\frac{c}{n}$
光从P从P点射入到第二次射出三棱镜经过的时间为:t=$\frac{PQ+QM+MN}{v}$
联立解得:t=$\frac{3L}{c}$
答:(1)三棱镜的折射率是$\sqrt{3}$;
(2)光从P点射入到第二次射出三棱镜经过的时间是$\frac{3L}{c}$.
点评 本题考查了折射定律的基本运用,关键要正确作出光路图,掌握全反射的条件,运用折射定律和几何关系进行求解.

练习册系列答案
相关题目
10. 如图所示,斜面体A静置于粗糙水平面上,小球B置于光滑的斜面上,用一轻绳拴住B,轻绳左端固定在竖直墙面上P处,初始时轻绳与斜面平行,若将轻绳左端从P处缓慢沿前面上移到P′处,斜面体始终处于静止状态,则在轻绳移动过程中( )
如图所示,斜面体A静置于粗糙水平面上,小球B置于光滑的斜面上,用一轻绳拴住B,轻绳左端固定在竖直墙面上P处,初始时轻绳与斜面平行,若将轻绳左端从P处缓慢沿前面上移到P′处,斜面体始终处于静止状态,则在轻绳移动过程中( )
 如图所示,斜面体A静置于粗糙水平面上,小球B置于光滑的斜面上,用一轻绳拴住B,轻绳左端固定在竖直墙面上P处,初始时轻绳与斜面平行,若将轻绳左端从P处缓慢沿前面上移到P′处,斜面体始终处于静止状态,则在轻绳移动过程中( )
如图所示,斜面体A静置于粗糙水平面上,小球B置于光滑的斜面上,用一轻绳拴住B,轻绳左端固定在竖直墙面上P处,初始时轻绳与斜面平行,若将轻绳左端从P处缓慢沿前面上移到P′处,斜面体始终处于静止状态,则在轻绳移动过程中( )| A. | 轻绳的拉力逐渐减小 | B. | 斜面体对小球的支持力逐渐减小 | ||
| C. | 斜面体对水平面的压力逐渐减小 | D. | 斜面体对水平面的摩擦力逐渐增大 |
7.历史上有些科学家曾这样定义直线运动的加速度:A=$\frac{{v}_{x}-{v}_{0}}{x}$,其中v0和vx分别表示某段位移x内的初速度和末速度.而现在物理学中加速度的定义式为a=$\frac{{v}_{t}-{v}_{0}}{t}$,下列说法正确的是( )
| A. | 对于加速直线运动,即初速度和加速度方向相同,若a不变,则A将变小 | |
| B. | 对于加速直线运动,即初速度和加速度方向相同,若A不变,则a将变小 | |
| C. | 若A不变,则物体在中间时刻的速度为$\frac{{v}_{0}+{v}_{x}}{2}$ | |
| D. | 若A不变,则物体在中间位置处的瞬时速度将小于物体中间时刻的瞬时速度 |
14.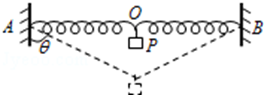 如图所示,长为2L的轻弹簧AB两端等高的固定在竖直墙面上,弹簧刚好处于原长,现在其中点O处轻轻地挂上一个质量为m的物体P后,物体向下运动,当它运动到最低点时,弹簧与竖直方向的夹角为θ,重力加速度为g,下列说法正确的是( )
如图所示,长为2L的轻弹簧AB两端等高的固定在竖直墙面上,弹簧刚好处于原长,现在其中点O处轻轻地挂上一个质量为m的物体P后,物体向下运动,当它运动到最低点时,弹簧与竖直方向的夹角为θ,重力加速度为g,下列说法正确的是( )
 如图所示,长为2L的轻弹簧AB两端等高的固定在竖直墙面上,弹簧刚好处于原长,现在其中点O处轻轻地挂上一个质量为m的物体P后,物体向下运动,当它运动到最低点时,弹簧与竖直方向的夹角为θ,重力加速度为g,下列说法正确的是( )
如图所示,长为2L的轻弹簧AB两端等高的固定在竖直墙面上,弹簧刚好处于原长,现在其中点O处轻轻地挂上一个质量为m的物体P后,物体向下运动,当它运动到最低点时,弹簧与竖直方向的夹角为θ,重力加速度为g,下列说法正确的是( )| A. | 向下运动的过程中,物体的加速度先增大后减小 | |
| B. | 向下运动的过程中,物体的机械能先增大后减小 | |
| C. | 物体在最低点时,弹簧的弹性势能为$\frac{mgL}{tanθ}$ | |
| D. | 物体在最低点时,弹簧中的弹力为$\frac{mg}{2cosθ}$ |
11. 如图所示,图甲为质点a和b做直线运动的位移-时间图象,图乙为质点c和d做直线运动的速度-时间图象,由图可知( )
如图所示,图甲为质点a和b做直线运动的位移-时间图象,图乙为质点c和d做直线运动的速度-时间图象,由图可知( )
 如图所示,图甲为质点a和b做直线运动的位移-时间图象,图乙为质点c和d做直线运动的速度-时间图象,由图可知( )
如图所示,图甲为质点a和b做直线运动的位移-时间图象,图乙为质点c和d做直线运动的速度-时间图象,由图可知( )| A. | 若t1时刻a、b两质点第一次相遇,则t2时刻两质点第二次相遇 | |
| B. | 若t1时刻c、d两质点第一次相遇,则t2时刻两质点第二次相遇 | |
| C. | t1到t2时间内,四个质点中只有b和d两个质点的运动方向发生改变 | |
| D. | t1到t2时间内,四个质点中只有b和d两个质点的速率先减小后增大 |
15. 某质点运动的v-t图象如图所示,下列有关该质点运动情况的判断,正确的是( )
某质点运动的v-t图象如图所示,下列有关该质点运动情况的判断,正确的是( )
 某质点运动的v-t图象如图所示,下列有关该质点运动情况的判断,正确的是( )
某质点运动的v-t图象如图所示,下列有关该质点运动情况的判断,正确的是( )| A. | 在第2s末,质点的速度方向发生改变 | |
| B. | 在0-2s时间内,质点做直线运动,在2s-4s时间内,质点做曲线运动 | |
| C. | 在0-2s时间内,质点的位移大小为2m | |
| D. | 在2-4s时间内,质点的加速度不断减小,方向也不断变化 |
 一辆总质量为20t的卡车在下坡时,司机突然发现刹车失灵,同时发动机又失去动力,此时速度表的示数为54km/h,卡车继续沿坡匀加速直行200m、下降高度50m后,刚好进入一条避险车道(如图所示),此时速度表的示数为90km/h.已知卡车在下坡过程中所受阻力恒定,g取10m/s2.
一辆总质量为20t的卡车在下坡时,司机突然发现刹车失灵,同时发动机又失去动力,此时速度表的示数为54km/h,卡车继续沿坡匀加速直行200m、下降高度50m后,刚好进入一条避险车道(如图所示),此时速度表的示数为90km/h.已知卡车在下坡过程中所受阻力恒定,g取10m/s2.