题目内容
(14分)如图所示，质量为m，边长为l的正方形平板与弹簧相连，弹簧的劲度系数为k，另一端固定于地面，平板处于平衡状态。质量为m的第一个小球从平台以一定速度垂直于平板的左边缘水平抛出，并与平板发生完全非弹性碰撞(设平台与板间高度差为h，抛出点在平板的左边缘正上方)。隔一段时间后，以相同速度抛出第二个小球。(假定在任何情况下平板始终保持水平，忽略平板在水平方向上的运动，且为方便计算起见，设h=3
)
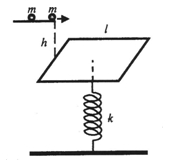
（1）求第一个小球落到平台上形成的振子系统的周期和频率；
（2）为了使第二个小球与平板不发生碰撞，其抛出速度的最小值为多少？
（3）在（2）的情况下，两小球抛出的时间差是多少？
解析：
（1）碰撞前后小球与平板，总质量为2m一起在新的平衡位置上下做简谐振动，如图中虚线所示
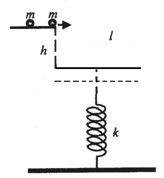
系统的周期为
系统的频率为
（式中ω为角频率）
（2）碰撞前，第一个小球在竖直方向的速度为
发生完全弹性碰撞，竖直方向有近似动量守恒
则碰撞后平板运动的速度为
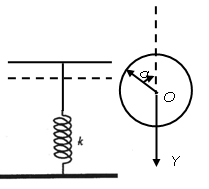
振子振幅为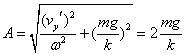
旋转参考矢量与y轴负方向的夹角满足
，则
设析运动到最低点位置时第二个小球正好下落到这一高度，则第二个小球下落用时
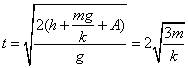
由此可以求出两者不发生碰撞时，第二个小球的最小抛出速度为
（3）第一个小球下落到平板用时
碰撞后平板从原平衡位置压缩到最低位置用时
设两球抛出的时间相差
，则
考虑到板往复一次用时，第二个小球抛出时间可以是振子系统运动时间大于一个周期后，则两小球抛出的时间差为
（n取非负整数）
练习册系列答案
相关题目
。一带正电
的小物块质量为m=0.5kg，它与水平轨道间的动摩擦因数均为μ=0.1。小物块在F=10N的水平恒力作用下从A点由静止开始运动，到达B点时撤去力F，小物块刚好能到达D点，试求：(g=10m/s2)
m/s2）求：
＝37°时立方体平衡且不动，作用在立方体上的水平推力F1应为多大？
。一带正电
的小物块质量为m=0.5kg，它与水平轨道间的动摩擦因数均为μ=0.1。小物块在F=10N的水平恒力作用下从A点由静止开始运动，到达B点时撤去力F，小物块刚好能到达D点，试求：(g=10m/s2)