题目内容
【题目】一根长直细杆长1.7m，从某一高处作自由落体运动，在下落过程中细杆通过一个1.75m高的窗口用时0.3s，求细杆刚下落时其下端到窗口上边缘的高度．（g取10m/s2 ， 窗口下边缘到地面的高度大于细杆的长度）
【答案】解：设杆下端到窗口上边缘的高度为h，运动时间为t，对从释放到杆的下边缘到达窗户上边缘过程运用位移时间关系公式，有： 
①
对从释放到杆的上边缘到窗户下边缘过程再次根据位移时间关系公式，有：
②
联立解得：
h=5m
t=1s
答：细杆刚下落时其下端到窗口上边缘的高度为5m．
【解析】设杆下端到窗口上边缘的高度，对从释放到杆的下边缘到达窗户上边缘过程运用位移时间关系公式 列式；再对从释放到杆的上边缘到窗户下边缘过程再次根据位移时间关系公式 列式；最后联立求解即可．
【考点精析】关于本题考查的自由落体运动，需要了解（1）条件:初速度为零，只受重力作用；（2）性质:是一种初速为零的匀加速直线运动，a=g才能得出正确答案．
【题目】甲乙两位同学利用穿过打点计时器的纸带来记录小车的运动，打点计时器所用电源的频率为50Hz．
（1）实验后，甲同学选择了一条较为理想的纸带，测量数据后，通过计算得到了小车运动过程中各计时时刻的速度如表格所示．
位置编号 | 0 | 1 | 2 | 3 | 4 | 5 |
时间：t/s | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
速度：v/ms﹣1 | 0.42 | 0.67 | 0.92 | 1.16 | 1.42 | 1.76 |
分析表中数据，在误差允许的范围内，小车做运动；由于此次实验的原始纸带没有保存，该同学想估算小车从位置0到位置5的位移，其估计算方法如下：x=（0.42×0.1+0.67×0.1+0.92×0.1+1.16×0.1+1.42×0.1）m，那么，该同学得到的位移 （选填“大于”、“等于”或“小于”）实际位移．
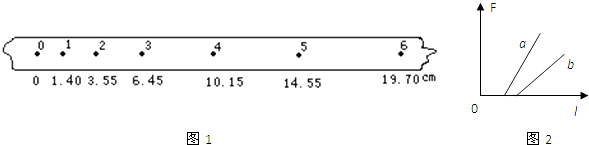
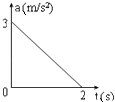
（2）乙同学的纸带如图1，按时间顺序取0、1、2、3、4、5、6七个计数点，每相邻的两计数点间都有四个点未画出．用刻度尺量出1、2、3、4、5、6点到0点的距离如图2所示（单位：cm）．由纸带数据计算可得计数点3所代表时刻的瞬时速度大小v3=m/s，小车的加速度大小a=m/s2 ． 
