题目内容
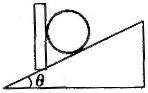
 如图所示,斜面的倾角θ=37°,斜面的底端有一个光滑的半圆形轨道与斜面底端B点相接.质量为m=50kg的物体,从斜面的顶点A处以v0=20m/s沿水平方向飞出,刚好落在斜面底端B处,其竖直速度立即变为零,然后进入半圆形轨道恰好能通过最高点C.(cos37°=0.8,sin37°=0.6,g取10m/s2,不计空气阻力)求:
如图所示,斜面的倾角θ=37°,斜面的底端有一个光滑的半圆形轨道与斜面底端B点相接.质量为m=50kg的物体,从斜面的顶点A处以v0=20m/s沿水平方向飞出,刚好落在斜面底端B处,其竖直速度立即变为零,然后进入半圆形轨道恰好能通过最高点C.(cos37°=0.8,sin37°=0.6,g取10m/s2,不计空气阻力)求:(1)半圆轨道的半径R;
(2)物体从A运动到B的时间t;
(3)如图,圆弧上点D与圆心连线与水平面平行,求小球过D点时对轨道的压力大小.
分析:(1)根据小球恰好到达最高点,得出最高点的速度,根据B点到最高点过程机械能守恒,求出半圆轨道的半径R.
(2)平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据竖直位移和水平位移之比得出运动的时间.
(3)根据机械能守恒求出到达D点的速度,通过径向的合力提供向心力求出小球过D点时对轨道的压力大小.
(2)平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据竖直位移和水平位移之比得出运动的时间.
(3)根据机械能守恒求出到达D点的速度,通过径向的合力提供向心力求出小球过D点时对轨道的压力大小.
解答:解:(1)设半圆形轨道的半径为R,因为物体恰好到达最高点,所以只有重力提供向心力.
设最高点的速度为v,则有:mg=m
.
从B点到最高点的过程,机械能守恒,则有:
mv∥2=
mv2+2mgR.
根据题意有:v∥=v0.
代入数据,联立解得:R=8m.
(2)从A到B的过程,做平抛运动,水平方向上有:x=v0t,竖直方向上有:y=
gt2.
因为
=tan37°
解得:t=
=3s.
(3)根据机械能守恒定律得:
mv∥2=
mvD2+mgR(1-sinθ)
代入数据,解得:vD=4
m/s.
根据牛顿第二定律得:N-mgsin37°=m
代入数据解得:N=2400N.
根据牛顿第三定律知,小球在D点对轨道压力大小为2400N.
答:(1)半圆轨道的半径R为8m;
(2)物体从A运动到B的时间t为3s;
(3)小球过D点时对轨道的压力大小为2400N.
设最高点的速度为v,则有:mg=m
| v2 |
| R |
从B点到最高点的过程,机械能守恒,则有:
| 1 |
| 2 |
| 1 |
| 2 |
根据题意有:v∥=v0.
代入数据,联立解得:R=8m.
(2)从A到B的过程,做平抛运动,水平方向上有:x=v0t,竖直方向上有:y=
| 1 |
| 2 |
因为
| y |
| x |
解得:t=
| 2v0tan37° |
| g |
(3)根据机械能守恒定律得:
| 1 |
| 2 |
| 1 |
| 2 |
代入数据,解得:vD=4
| 21 |
根据牛顿第二定律得:N-mgsin37°=m
| vD2 |
| R |
代入数据解得:N=2400N.
根据牛顿第三定律知,小球在D点对轨道压力大小为2400N.
答:(1)半圆轨道的半径R为8m;
(2)物体从A运动到B的时间t为3s;
(3)小球过D点时对轨道的压力大小为2400N.
点评:本题考查了圆周运动和平抛运动的综合,涉及到牛顿第二定律和机械能守恒定律的运用,知道圆周运动向心力的来源和平抛运动在水平方向和竖直方向上的运动规律是解决本题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
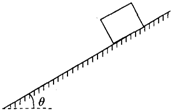 如图所示,斜面的倾角θ=37°.一个质量m=1.0kg的物体,从静止开始沿斜面下滑.在开始运动后的最初2.0s内,物体下滑的距离为4.0m.不计空气阻力.计算时重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.
如图所示,斜面的倾角θ=37°.一个质量m=1.0kg的物体,从静止开始沿斜面下滑.在开始运动后的最初2.0s内,物体下滑的距离为4.0m.不计空气阻力.计算时重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.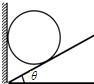 如图所示,斜面的倾角为θ,圆柱体质量为m.若把重力沿垂直于墙面和垂直于斜面两个方向分解,则重力垂直于斜面的分力大小为
如图所示,斜面的倾角为θ,圆柱体质量为m.若把重力沿垂直于墙面和垂直于斜面两个方向分解,则重力垂直于斜面的分力大小为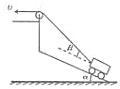 如图所示,斜面的倾角为α,人用跨过定滑轮的绳子拉小车.现人以速度v匀速拉动绳子,当拉小车的绳子与斜面的夹角为β时,小车沿斜面运动的速度为( )
如图所示,斜面的倾角为α,人用跨过定滑轮的绳子拉小车.现人以速度v匀速拉动绳子,当拉小车的绳子与斜面的夹角为β时,小车沿斜面运动的速度为( )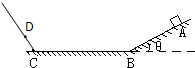 如图所示,斜面的倾角θ=37°,一物块从斜面A点由静止释放.物块质量m=10kg,物块与水平面的动摩擦因数μ=0.4,其余部分光滑,不计物块滑至B、C点时由于碰撞的能量损失,最后能够上升到D点.已知AB高度差H=1.8m,CD高度差为h=0.6m,(取g=10m/s2,sin37°=0.6,cos37°=0.8)( )
如图所示,斜面的倾角θ=37°,一物块从斜面A点由静止释放.物块质量m=10kg,物块与水平面的动摩擦因数μ=0.4,其余部分光滑,不计物块滑至B、C点时由于碰撞的能量损失,最后能够上升到D点.已知AB高度差H=1.8m,CD高度差为h=0.6m,(取g=10m/s2,sin37°=0.6,cos37°=0.8)( )