题目内容
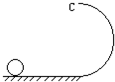如图所示，一个小球质量为m，静止在光滑的轨道上，现以水平力击打小球，使小球能够通过半径为R的竖直光滑轨道的最高点C，则水平力对小球所做的功至少为（ ）分析：根据牛顿第二定律求出小球通过最高点C的最小速度，通过动能定理求出水平了对小球做功的最小值．
解答：解：根据牛顿第二定律得，mg=m
，解得vC=
则根据动能定理得，W-mg?2R=
mvc2，解得W=2.5mgR．故B正确，A、C、D错误．
故选B．
| vc2 |
| R |
| gR |
则根据动能定理得，W-mg?2R=
| 1 |
| 2 |
故选B．
点评：本题考查了牛顿第二定律和动能定理的综合运用，知道小球越过最高点的临界情况，通过动定理进行求解．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图所示，一个小球从高处自由下落到达A点与一个轻质弹簧相撞，弹簧被压缩．在球与弹簧接触，到弹簧被压缩到最短的过程中，关于球的动能、重力势能、弹簧的弹性势能的说法中正确的是（ ）
如图所示，一个小球从高处自由下落到达A点与一个轻质弹簧相撞，弹簧被压缩．在球与弹簧接触，到弹簧被压缩到最短的过程中，关于球的动能、重力势能、弹簧的弹性势能的说法中正确的是（ ）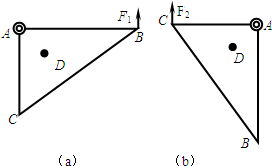
（2013?浦东新区一模）如图所示，一个轻质直角形薄板ABC，AB=0.80m，AC=0.60m，在A点固定一垂直于薄板平面的光滑转动轴，在薄板上D点固定一个质量为m=0.40kg的小球，现用测力计竖直向上拉住B点，使AB水平，如图（a），测得拉力F1=2.0N；再用测力计竖直向上拉住C点，使AC水平，如图（b），测得拉力F2=2.0N（g取10m/s2，sin37°=0.6，cos37°=0.8）．求：
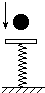如图所示，一个小球从高处自由下落，撞到一个轻质弹簧上，从球与弹簧按触到将弹簧压缩到最短的过程中，弹簧的弹性势能