题目内容
14.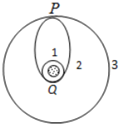 发射地球同步卫星要经过三个阶段:先将卫星发射至 近地圆轨道1,然后使其沿椭圆轨道2运行,最后将卫星送入同步圆轨道3.轨道1、2相切于Q点,轨道2、3相切于P点,如图所示.当卫星分别在1、2、3轨道上正常运行时,以下说法正确的是( )
发射地球同步卫星要经过三个阶段:先将卫星发射至 近地圆轨道1,然后使其沿椭圆轨道2运行,最后将卫星送入同步圆轨道3.轨道1、2相切于Q点,轨道2、3相切于P点,如图所示.当卫星分别在1、2、3轨道上正常运行时,以下说法正确的是( )| A. | 卫星在轨道1上经过Q点时的加速度等于它在轨道2上经过Q点时的加速度 | |
| B. | 卫星在轨道1上经过Q点时的速度等于它在轨道2上经过Q点时的速度 | |
| C. | 卫星在轨道3上的速度大于它在轨道1上的速度 | |
| D. | 卫星在轨道3上的周期大于它在轨道1上的周期 |
分析 根据人造卫星的万有引力等于向心力,列式求出线速度、角速度、和向心力的表达式进行讨论即可.
解答 解:A、根据牛顿第二定律和万有引力定律得:a=$\frac{GM}{{r}^{2}}$,
所以卫星在轨道1上经过Q点时的加速度等于它在轨道2上经过Q点时的加速度,故A正确;
B、由题意可知,卫星在轨道1上做匀速圆周运动,而在在轨道2上做椭圆运动,则在同一位置Q点,在2轨道上要做离心运动,则在轨道1上的经过Q点时的速度小于它在轨道2上经过Q点时的速度,故B错误;
C、由人造卫星的万有引力等于向心力$\frac{GM}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$,
得v=$\sqrt{\frac{GM}{r}}$,
所以卫星在轨道3上的速度小于它在轨道1上的速度,故C错误;
D、由开普勒第三定律$\frac{{R}^{3}}{{T}^{2}}$=k得卫星在轨道3上的周期大于它在轨道1上的周期,故D正确;
故选:AD.
点评 本题关键抓住万有引力提供向心力,先列式求解出线速度和角速度的表达式,再进行讨论,注意在同一位置的加速度大小相等,并理解离心运动的应用.

练习册系列答案
相关题目
1.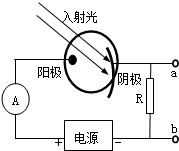 如图为光电管工作原理示意图,阴极材料的逸出功为W,入射光的光子能量为hv,能发生光电效应,则( )
如图为光电管工作原理示意图,阴极材料的逸出功为W,入射光的光子能量为hv,能发生光电效应,则( )
 如图为光电管工作原理示意图,阴极材料的逸出功为W,入射光的光子能量为hv,能发生光电效应,则( )
如图为光电管工作原理示意图,阴极材料的逸出功为W,入射光的光子能量为hv,能发生光电效应,则( )| A. | hv<W | |
| B. | 光电子在管内运动过程中电势能减小 | |
| C. | 减弱入射光强度,ab两端的电压减小 | |
| D. | 入射光的频率变高,所有出射光电子的动能都增大 |
5.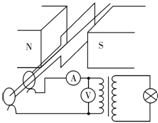 某兴趣小组用实验室的手摇发电机和理想变压器给一个灯泡供电,电路如图,当线圈以较大的转速n匀速转动时,电压表示数是U1,额定电压为U2的灯泡正常发光,灯泡正常发光时电功率为P,手摇发电机的线圈电阻是r,则有( )
某兴趣小组用实验室的手摇发电机和理想变压器给一个灯泡供电,电路如图,当线圈以较大的转速n匀速转动时,电压表示数是U1,额定电压为U2的灯泡正常发光,灯泡正常发光时电功率为P,手摇发电机的线圈电阻是r,则有( )
 某兴趣小组用实验室的手摇发电机和理想变压器给一个灯泡供电,电路如图,当线圈以较大的转速n匀速转动时,电压表示数是U1,额定电压为U2的灯泡正常发光,灯泡正常发光时电功率为P,手摇发电机的线圈电阻是r,则有( )
某兴趣小组用实验室的手摇发电机和理想变压器给一个灯泡供电,电路如图,当线圈以较大的转速n匀速转动时,电压表示数是U1,额定电压为U2的灯泡正常发光,灯泡正常发光时电功率为P,手摇发电机的线圈电阻是r,则有( )| A. | 电流表的示数是$\frac{P}{{U}_{1}}$ | |
| B. | 变压器原副线圈的匝数比是U2:U1 | |
| C. | 变压器输入电压的瞬时值μ=U2sin2πnt | |
| D. | 手摇发电机线圈中产生的电动势最大值是Em=$\sqrt{2}$(U1+$\frac{Pr}{{U}_{1}}$) |
2.质量分别为m、M(m<M)的两个物体,M放在光滑水平面上,m放在粗糙水平面上,在相同水平推力F作用下,两物体移动了相同的位移l,两个物体所做的功的关系是( )
| A. | 推力F对两个物体所做的功一样多 | |
| B. | 推力F对在光滑水平面上运动的M所做的功多 | |
| C. | 推力F对在粗糙水平面上运动的m所做的功多 | |
| D. | 做功的多少与物体通过这段位移的时间无关 |
9.根据如图所示的振动图象,算出t1=0.5s时刻振子对平衡位置的位移,正确的是( )
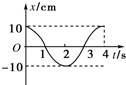

| A. | 5$\sqrt{2}$ cm | B. | 5 cm | C. | -5$\sqrt{2}$ cm | D. | 6 cm |
3.只知道下列那一组物理量,就可以估算出气体中分子间的平均距离( )
| A. | 阿伏加徳罗常数,该气体的摩尔质量和质量 | |
| B. | 阿伏加徳罗常数,该气体的摩尔质量和密度 | |
| C. | 阿伏加徳罗常数,该气体的质量和体积 | |
| D. | 该气体的质量、体积和摩尔质量 |
4.关于功的概念,下列说法正确的是( )
| A. | 物体受力越大,位移越大,力对物体做功越多 | |
| B. | 摩擦力一定对物体做负功 | |
| C. | 作用力和反作用力做的功一定大小相等,且两者的代数和为零 | |
| D. | 某个力对物体做负功,力的方向不一定与物体的位移方向相反 |
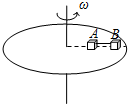 如图所示,在匀速转动的水平圆盘上,沿半径方向放置两个用细线相连的质量均为m的小物体A、B,它们到转轴的距离分别为rA=20cm,rB=30cm,A、B与盘间最大静摩擦力均为重力的k=0.4倍,现极其缓慢的增加转盘的角速度,试求:(答案可用根号表示)
如图所示,在匀速转动的水平圆盘上,沿半径方向放置两个用细线相连的质量均为m的小物体A、B,它们到转轴的距离分别为rA=20cm,rB=30cm,A、B与盘间最大静摩擦力均为重力的k=0.4倍,现极其缓慢的增加转盘的角速度,试求:(答案可用根号表示)