题目内容
19.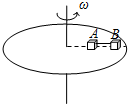 如图所示,在匀速转动的水平圆盘上,沿半径方向放置两个用细线相连的质量均为m的小物体A、B,它们到转轴的距离分别为rA=20cm,rB=30cm,A、B与盘间最大静摩擦力均为重力的k=0.4倍,现极其缓慢的增加转盘的角速度,试求:(答案可用根号表示)
如图所示,在匀速转动的水平圆盘上,沿半径方向放置两个用细线相连的质量均为m的小物体A、B,它们到转轴的距离分别为rA=20cm,rB=30cm,A、B与盘间最大静摩擦力均为重力的k=0.4倍,现极其缓慢的增加转盘的角速度,试求:(答案可用根号表示)(1)当细线上开始出现张力时,圆盘的角速度ω1;
(2)当A开始滑动时,圆盘的角速度ω;
(3)当A即将滑动时,烧断细线,A、B运动状态如何?
分析 (1)抓住最大静摩擦力提供向心力,根据牛顿第二定律求出细线出现张力时圆盘的角速度.
(2)当A开始滑动时,B靠拉力和最大静摩擦力提供向心力,A靠最大静摩擦力和拉力的合力提供向心力,结合牛顿第二定律列式求解.
(3)根据静摩擦力和向心力的关系判断A、B的运动规律.
解答 解:(1)当细线上开始出现张力时,B与圆盘之间的静摩擦力达到最大值.
对B:$kmg=m{r}_{B}{{ω}_{1}}^{2}$,
即${ω}_{1}=\sqrt{\frac{kr}{{r}_{B}}}=\sqrt{\frac{0.4×10}{0.3}}rad/s=\frac{2}{3}\sqrt{30}$rad/s.
(2)当A开始滑动时,A、B所受静摩擦力均达最大,设此时细绳张力为T:
对B:$T+kmg=m{r}_{B}{ω}^{2}$,
对A:$kmg-T=m{r}_{A}{ω}^{2}$,
联立解得:$ω=\sqrt{\frac{2kg}{{r}_{A}+{r}_{B}}}=\sqrt{\frac{2×0.4×10}{0.2+0.3}}=4rad/s$.
(3)烧断细线时,绳的拉力消失,B所受静摩擦力不足以提供所需向心力,故将远离圆心;对A,拉力消失后,静摩擦力变小,提供所需向心力,故继续做圆周运动
答:(1)当细线上开始出现张力时,圆盘的角速度为$\frac{2}{3}\sqrt{30}rad/s$;
(2)当A开始滑动时,圆盘的角速度为4rad/s;
(3)B做离心运动,A继续做圆周运动.
点评 解决本题的关键知道A、B做圆周运动向心力的来源,抓住临界状态,结合牛顿第二定律进行求解.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
6.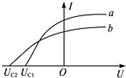 用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图.则这两种光( )
用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图.则这两种光( )
 用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图.则这两种光( )
用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图.则这两种光( )| A. | a光的频率更大 | |
| B. | 在增大电压U时,光电流一定都会增大 | |
| C. | 照射该光电管时a光单位时间发生的光电子数多 | |
| D. | 照射该光电管时b光使其逸出的光电子最大初动能大 |
14.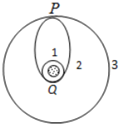 发射地球同步卫星要经过三个阶段:先将卫星发射至 近地圆轨道1,然后使其沿椭圆轨道2运行,最后将卫星送入同步圆轨道3.轨道1、2相切于Q点,轨道2、3相切于P点,如图所示.当卫星分别在1、2、3轨道上正常运行时,以下说法正确的是( )
发射地球同步卫星要经过三个阶段:先将卫星发射至 近地圆轨道1,然后使其沿椭圆轨道2运行,最后将卫星送入同步圆轨道3.轨道1、2相切于Q点,轨道2、3相切于P点,如图所示.当卫星分别在1、2、3轨道上正常运行时,以下说法正确的是( )
 发射地球同步卫星要经过三个阶段:先将卫星发射至 近地圆轨道1,然后使其沿椭圆轨道2运行,最后将卫星送入同步圆轨道3.轨道1、2相切于Q点,轨道2、3相切于P点,如图所示.当卫星分别在1、2、3轨道上正常运行时,以下说法正确的是( )
发射地球同步卫星要经过三个阶段:先将卫星发射至 近地圆轨道1,然后使其沿椭圆轨道2运行,最后将卫星送入同步圆轨道3.轨道1、2相切于Q点,轨道2、3相切于P点,如图所示.当卫星分别在1、2、3轨道上正常运行时,以下说法正确的是( )| A. | 卫星在轨道1上经过Q点时的加速度等于它在轨道2上经过Q点时的加速度 | |
| B. | 卫星在轨道1上经过Q点时的速度等于它在轨道2上经过Q点时的速度 | |
| C. | 卫星在轨道3上的速度大于它在轨道1上的速度 | |
| D. | 卫星在轨道3上的周期大于它在轨道1上的周期 |
11.如图甲所示为理想调压变压器,原线圈A、B端的输入电压如图乙所示,则当此变压器工作时,以下说法正确的是( )
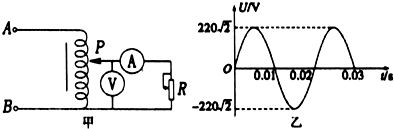

| A. | 若滑动触头P处于某一确定位置,当变阻器R的滑动触头下滑时,电流表示数将变大 | |
| B. | 若滑动触头P处于某一确定位置,当变阻器R的滑动触头上滑时,电压表示数增大 | |
| C. | 若滑动触头P和变阻器R的滑动触头同时上移,则电流表示数一定变大 | |
| D. | 若变阻器最大阻值为100Ω,且变阻器R的滑动触头置于最上端,则在滑动触头P滑动的过程中,电流表的电流变化范围为0~2.2 A |
9.对于万有引力定律数学表达式:F=G$\frac{{m}_{1}{m}_{2}}{{r}^{2}}$,下列说法正确的是( )
| A. | 公式中G为引力常数,是人为规定的 | |
| B. | r趋近于0时,万有引力趋近于无穷大 | |
| C. | m1、m2受到的万有引力总是大小相等的,与m1、m2是否相等无关 | |
| D. | m1、m2受到的万有引力总是大小相等方向相反,是一对平衡力 |

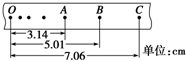 在“验证机械能守恒定律”的实验中,打点计时器所用电源频率为50Hz,当地重力加速度的值为9.80m/s2,测得所用重物的质量为1.00kg.甲、乙、丙三位同学分别用同一装置打出三条纸带,量出各纸带上第1、2两点间的距离分别为0.18cm、0.19cm和0.25cm.可见其中肯定有一位同学在操作上有错误,错误操作是丙同学先放开纸带后接通电源.若按实验要求正确地选出纸带进行测量,测得连续三点A、B、C到第一个点的距离如图1所示(相邻计数点时间间隔为0.02s)那么:
在“验证机械能守恒定律”的实验中,打点计时器所用电源频率为50Hz,当地重力加速度的值为9.80m/s2,测得所用重物的质量为1.00kg.甲、乙、丙三位同学分别用同一装置打出三条纸带,量出各纸带上第1、2两点间的距离分别为0.18cm、0.19cm和0.25cm.可见其中肯定有一位同学在操作上有错误,错误操作是丙同学先放开纸带后接通电源.若按实验要求正确地选出纸带进行测量,测得连续三点A、B、C到第一个点的距离如图1所示(相邻计数点时间间隔为0.02s)那么: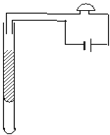 如图所示为一简易火灾报警装置,其原理是:竖直放置的试管中装有水银,当温度升高时,水银柱上升,使电路导通,蜂鸣器发出报警的响声.已知27℃时,空气柱长度L1为20cm.此时水银柱上表面与导线下端的距离L2为10cm.管内水银柱的高度h为8cm,大气压强为75cmHg.
如图所示为一简易火灾报警装置,其原理是:竖直放置的试管中装有水银,当温度升高时,水银柱上升,使电路导通,蜂鸣器发出报警的响声.已知27℃时,空气柱长度L1为20cm.此时水银柱上表面与导线下端的距离L2为10cm.管内水银柱的高度h为8cm,大气压强为75cmHg.